Question

【题目】一矩形的一边在轴上，另两个顶点在函数的图像上，如图，则此矩形绕轴旋转而成的几何体的体积的最大值是（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

用表示圆柱的体积可得，由基本不等式可求其最大值，从而得到正确的选项.

因为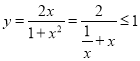当且仅当时取等号，所以.

因为矩形绕轴旋转一周旋转得到一个圆柱，

设点的坐标为，点的坐标为，

则圆柱的底面圆的半径为，高为，

因为，即，

所以，所以，

所以，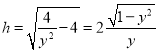

所以圆柱得体积为，

当且仅当时取等号，

所以矩形绕轴旋转而成的几何体的体积的最大值是，

故选：A．

【点晴】

本题主要考查了空间几何体的体积的计算、基本不等式的应用，解答的关键确定的值，属于中档试题，同时着重考查了转化与化归的思想方法及数形结合的思想方法的应用，本题的解答中先求出的范围，再设出点的坐标，根据两点的纵坐标相等得到，再求出高，根据图形旋转得到一个圆柱，根据圆柱的体积公式得到关系式，利用基本不等式求最值．