
【题目】已知函数![]()
若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线 ![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(Ⅱ)讨论函数 ![]() 的单调性;
的单调性;
(Ⅲ)当 ![]() 时,记函数
时,记函数 ![]() 的最小值为
的最小值为 ![]() ,求证:
,求证:![]() ;
;
【答案】(1) ![]() 或
或![]() .
.
(2) ![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减; 当
上单调递减; 当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(3)证明见解析.
【解析】分析:(Ⅰ)求出![]() ,根据
,根据![]() 可求得实数
可求得实数![]() 的值;(Ⅱ)求出
的值;(Ⅱ)求出![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(Ⅲ)由(Ⅱ)可知,当
的减区间;(Ⅲ)由(Ⅱ)可知,当![]() 时,函数
时,函数![]() 的最小值
的最小值![]() ,故
,故![]() ,利用导数研究函数的单调性,可得当
,利用导数研究函数的单调性,可得当![]() 时,
时,![]() ,从而可得结果.
,从而可得结果.
详解:(Ⅰ)由已知可知![]() 的定义域为
的定义域为![]() ,
,
![]() 根据题意可得,
根据题意可得,![]()
![]()
![]() 或
或![]()
(Ⅱ)![]()
①![]() 时,由
时,由![]() 可得
可得![]()
由![]() 可得
可得![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
②当![]() 时,
时,
由![]() 可得
可得![]()
由![]() 可得
可得![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
(Ⅲ)由(Ⅱ)可知,当![]() 时,函数
时,函数![]() 的最小值
的最小值![]()
故![]()
则![]()
令![]() 可得
可得![]()
![]()
当![]() 变化时,
变化时,![]() 的变化情况如表:
的变化情况如表:
|
|
|
|
| - | 0 | - |
| 增 | 极大值 | 减 |
![]() 是
是![]() 在
在![]() 上的唯一的极大值,从而是
上的唯一的极大值,从而是![]() 的最大值点,
的最大值点,
当![]() 时,
时,![]()
![]() 时,
时,![]()


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】设命题p:x∈[1,2], ![]() ﹣lnx﹣a≥0,命题q:x0∈R,使得x02+2ax0﹣8﹣6a≤0,如果命题“p或q”是真命题,命题“p且q”是假命题,求实数a的取值范围.
﹣lnx﹣a≥0,命题q:x0∈R,使得x02+2ax0﹣8﹣6a≤0,如果命题“p或q”是真命题,命题“p且q”是假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-7x+6<0},B={x|4-t<x<t},R为实数集.
(1)当t=4时,求A∪B及A∩RB;
(2)若A∪B=A,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)求![]() 的值;
的值;
(2)求函数![]() 的极小值;
的极小值;
(3)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某算法的算法框图如图所示,若将输出的(x,y)值依次记为(x1 , y1),(x2 , y2),…,(xn , yn),…,则程序结束时,共输出(x,y)的组数为( ) ![]()
A.1006
B.1007
C.1008
D.1009
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A套餐 | 50% | 25% | 25% |
B套餐 | 80% | 0 | 20% |
C套餐 | 50% | 50% | 0 |
D套餐 | 40% | 20% | 40% |
(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.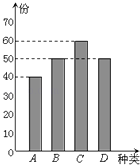
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线上![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]()
(1)求圆C的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与圆C交于
与圆C交于![]() 两点,且
两点,且![]() 的面积为
的面积为![]() (O为坐标原点),若存在,求出直线
(O为坐标原点),若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)设不等式(x﹣a)(x+a﹣2)<0的解集为N, ![]() ,若x∈N是x∈M的必要条件,求a的取值范围.
,若x∈N是x∈M的必要条件,求a的取值范围.
(2)已知命题:“x∈{x|﹣1<x<1},使等式x2﹣x﹣m=0成立”是真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次抽样调查中测得样本的5个样本点,数值如下表:
| 0.25 | 0.5 | 1 | 2 | 4 |
| 16 | 12 | 5 | 2 | 1 |
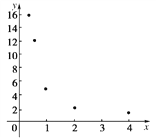
(1)根据散点图判断,![]() 哪一个适宜作为
哪一个适宜作为![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果试建立![]() 与
与![]() 之间的回归方程.(注意
之间的回归方程.(注意![]() 或
或![]() 计算结果保留整数)
计算结果保留整数)
(3)由(2)中所得设z=![]() +
+![]() 且
且![]() ,试求z的最小值。
,试求z的最小值。
参考数据及公式如下:
![]() ,
,![]() ,
,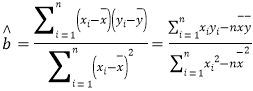
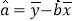
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com