
【题目】已知等差数列![]() 的公差不为零,
的公差不为零,![]() ,且
,且![]() 成等比数列.
成等比数列.
(1)求![]() 的通项公式;
的通项公式;
(2)求![]() .
.
【答案】(1)![]() (1)Sn=-3n2+28n
(1)Sn=-3n2+28n
【解析】
(1)设等差数列{an}的公差为d≠0,利用成等比数列的定义可得,a112=a1a1,再利用等差数列的通项公式可得(a1+10d)2=a1(a1+12d),化为d(2a1+25d)=0,解出d即可得到通项公式an;
(2)由(1)可得a3n-2=-2(3n-2)+27=-6n+31,可知此数列是以25为首项,-6为公差的等差数列.利用等差数列的前n项和公式即可得出a1+a4+a7+…+a3n-2.
(1)设{an}的公差为d.由题意,a112=a1a13,即(a1+10d)2=a1(a1+12d).
于是d(2a1+25d)=0.又a1=25,所以d=0(舍去),d=-2.故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.
由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列.
从而Sn=![]() (a1+a3n-2)=
(a1+a3n-2)=![]() (-6n+56)=-3n2+28n.
(-6n+56)=-3n2+28n.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线C1的参数方程为  (θ为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,两坐标系取相同的单位长度,曲线C2的极坐标方程为ρ=﹣2sin(θ+
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,两坐标系取相同的单位长度,曲线C2的极坐标方程为ρ=﹣2sin(θ+ ![]() ).
).
(1)把曲线C1的参数方程化为极坐标方程;
(2)求曲线C1与C2的交点M(ρ1 , θ1)的极坐标,其中ρ1≤0,0≤θ1<2π.
查看答案和解析>>
科目:高中数学 来源: 题型:
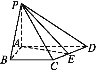
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
求证:CD⊥平面PAE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F,H分别是正方体ABCD-A1B1C1D1的棱CC1,AA1的中点,棱长为![]() ,
,

(1)求证:平面BDF∥平面B1D1H.
(2)求正方体![]() 外接球的表面积。
外接球的表面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在同一个平面内,向量 ![]() ,
, ![]() ,
, ![]() 的模分别为1,1,
的模分别为1,1, ![]() ,
, ![]() 与
与 ![]() 的夹角为α,且tanα=7,
的夹角为α,且tanα=7, ![]() 与
与 ![]() 的夹角为45°.若
的夹角为45°.若 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),则m+n= .
(m,n∈R),则m+n= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆的中心在原点,焦点在![]() 轴上,点
轴上,点![]() 是椭圆上的一点,
是椭圆上的一点,![]() 在
在![]() 轴上的射影恰为椭圆的左焦点,
轴上的射影恰为椭圆的左焦点,![]() 与中心
与中心![]() 的连线平行于右顶点与上顶点的连线,且左焦点与左顶点的距离等于
的连线平行于右顶点与上顶点的连线,且左焦点与左顶点的距离等于![]() ,试求椭圆的离心率及其方程.
,试求椭圆的离心率及其方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com