
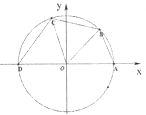
【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC= ![]() .
. 
(1)若点B( ![]() ,
, ![]() ),求cos∠AOC的值;
),求cos∠AOC的值;
(2)设∠AOB=x(0<x< ![]() ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
【答案】
(1)解:∵B( ![]() ,
, ![]() ),
),
∴cos∠AOB= ![]() ,sin∠AOB=
,sin∠AOB= ![]() ;
;
∴cos∠AOC=cos(∠AOB+∠BOC)
=cos∠AOBcos∠BOC﹣sin∠AOBsin∠BOC
= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]()
= ![]() ;
;
(2)解:等腰三角形AOB中,求得|AB|=2|OB|sin ![]() =2sin
=2sin ![]() ,
,
等腰三角形COD中,求得
|CD|=2|OC|sin ![]() =2sin(
=2sin( ![]() ﹣
﹣ ![]() );
);
∴y=|AB|+|BC|+|CD|+|DA|
=3+2sin ![]() +2sin(
+2sin( ![]() ﹣
﹣ ![]() )
)
=3+2sin( ![]() +
+ ![]() );
);
由0<x< ![]() 得,当
得,当 ![]() +
+ ![]() =
= ![]() ,
,
即x= ![]() 时,y取得最大值5
时,y取得最大值5
【解析】(1)由三角函数的定义,写出cos∠AOB与sin∠AOB的值,再计算cos∠AOC的值;(2)根据等腰三角形的知识,求出|AB|、|CD|的值,再写出函数y的解析式,求出y的最大值即可.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:参数方程与极坐标系
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为倾斜角),以坐标原点O为极点,
为倾斜角),以坐标原点O为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的直角坐标方程,并 求C的焦点F的直角坐标;
的直角坐标方程,并 求C的焦点F的直角坐标;
(2)已知点![]() ,若直线
,若直线![]() 与C相交于A,B两点,且
与C相交于A,B两点,且![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx2﹣mx﹣1.
(1)若对于x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于x∈[1,3],f(x)<5﹣m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,M在线段
,M在线段![]() 上,且
上,且![]() .
.
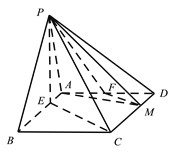
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段AD上确定一点F,使得平面![]() 平面PAB,并求三棱锥
平面PAB,并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将直线2x﹣y+λ=0沿x轴向左平移1个单位,所得直线与圆x2+y2+2x﹣4y=0相切,则实数λ的值为( )
A.﹣3或7
B.﹣2或8
C.0或10
D.1或11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算题。
(1)已知等比数列{an}中,a1=﹣1,a4=64,求q与S4
(2)已知等差数列{an}中,a1= ![]() ,d=﹣
,d=﹣ ![]() ,Sn=﹣15,求n及an .
,Sn=﹣15,求n及an .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场拟对某商品进行促销,现有两种方案供选择,每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4,第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令![]() 表示实施方案
表示实施方案![]() 的第二个月的销量是促销前销量的倍数.
的第二个月的销量是促销前销量的倍数.
(Ⅰ)求![]() ,
, ![]() 的分布列;
的分布列;
(Ⅱ)不管实施哪种方案, ![]() 与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com