
【题目】二次函数![]() 的图象顶点为
的图象顶点为![]() ,且图象在
,且图象在![]() 轴上截得的线段长为8.
轴上截得的线段长为8.
(1)求函数![]() 的解析式;
的解析式;
(2)令![]() .
.
(ⅰ)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(ⅱ)若![]() 时,不等式
时,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)(i)分类讨论,详见解析;(ii)
;(2)(i)分类讨论,详见解析;(ii)![]() .
.
【解析】
(1)先设二次函数![]() 为顶点式,然后根据其顶点为
为顶点式,然后根据其顶点为![]() ,可知函数
,可知函数![]() 的解析式为
的解析式为![]() ,由图象在
,由图象在![]() 轴上截得的线段长为8,利用韦达定理即可解.
轴上截得的线段长为8,利用韦达定理即可解.
(2)(i)先求出函数![]() 的解析式,再根据
的解析式,再根据![]() ,分类讨论函数
,分类讨论函数![]() 的对称轴
的对称轴![]() ,当
,当![]() 时,函数
时,函数![]() 最小值的情况.
最小值的情况.
(ii)不等式![]() 恒成立转化为函数
恒成立转化为函数![]() 在区间
在区间![]() 上最大值小于等于17,再利用分类讨论思想讨论a的范围即可解.
上最大值小于等于17,再利用分类讨论思想讨论a的范围即可解.
解:(1)由题意设![]() ,与
,与![]() 轴的交点坐标为
轴的交点坐标为![]() ,
,![]()
∴![]() ,∵
,∵![]() ,
,
由韦达定理可得![]() .
.
∴![]() ,
,
∴![]() ,∴
,∴![]()
(2)![]() ,
,
对称轴为![]() ,
,
(ⅰ)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 为单调减函数,
为单调减函数,
∴![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上为单调增函数,在区间
上为单调增函数,在区间![]() 上为单调减函数,
上为单调减函数,
![]() .
.
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上为单调增函数,
上为单调增函数,
在区间![]() 上为单调减函数,∴
上为单调减函数,∴![]() .
.
当![]() 时,
时,![]() .
.
∴函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
(ⅱ)①当![]() 时,
时,![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() ,显然成立,∴
,显然成立,∴![]() .
.
②当![]() 时,
时,![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() ,
,
即![]() ,∴
,∴![]() .
.
③当![]() 时,
时,![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() ,
,
即![]() ,这与
,这与![]() 矛盾,故舍去.
矛盾,故舍去.
综上所述,![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】设a,b,c表示三条不同的直线,M表示平面,给出下列四个命题:其中正确命题的个数有( )
①若a//M,b//M,则a//b;
②若bM,a//b,则a//M;
③若a⊥c,b⊥c,则a//b;
④若a//c,b//c,则a//b.
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,其岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.以北京为例,2018年这几类工作岗位的薪资(单位:万元/月)情况如下表所示.
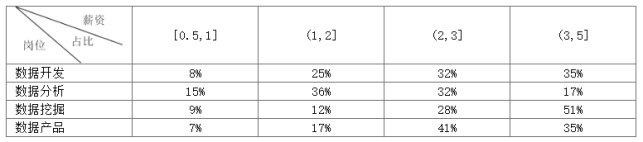
由表中数据可得各类岗位的薪资水平高低情况为
A. 数据挖掘>数据开发>数据产品>数据分析B. 数据挖掘>数据产品>数据开发>数据分析
C. 数据挖掘>数据开发>数据分析>数据产品D. 数据挖掘>数据产品>数据分析>数据开发
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com