
求“方程 的解”有如下解题思路:设
的解”有如下解题思路:设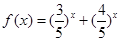 ,则
,则 在
在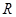 上单调递减,且
上单调递减,且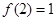 ,所以原方程有唯一解
,所以原方程有唯一解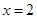 .类比上述解题思路,方程
.类比上述解题思路,方程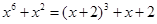 的解集为 .
的解集为 .
科目:高中数学 来源: 题型:填空题
挪威数学家阿贝尔曾经根据阶梯形图形的两种不同分割(如下图),利用它们的面积关系发现了一个重要的恒等式——阿贝尔公式: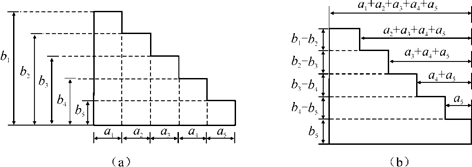
a1b1+a2b2+a3b3+…+anbn=L1(b1-b2)+L2(b2-b3)+L3(b3-b4)+…+Ln-1(bn-1-bn)+Lnbn,其中L1=a1,则
(Ⅰ)L3= ;
(Ⅱ)Ln= .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图,在圆内:画1条弦,把圆分成2部分;画2条相交的弦,把圆分成4部分,画3条两两相交的弦,把圆最多分成7部分;…,画 条两两相交的弦,把圆最多分成 部分.
条两两相交的弦,把圆最多分成 部分.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
现有一个关于平面图形的命题:如图所示,同一个平面内有两个变长都是a的正方形,其中一个正方形的某起点在另一个正方形的中心,则这两个正方形重叠部分的面积恒为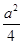 ,类比到空间,有两个棱长为a的正方体,其中某一个正方体的某顶点在另一个正方体的中心,则这两个正方体的重叠部分的体积恒为___
,类比到空间,有两个棱长为a的正方体,其中某一个正方体的某顶点在另一个正方体的中心,则这两个正方体的重叠部分的体积恒为___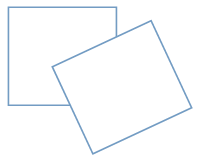
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知一个关于正整数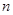 的命题
的命题 满足“若
满足“若 时命题
时命题 成立,则
成立,则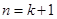 时命题
时命题 也成立”.有下列判断:
也成立”.有下列判断:
(1)当 时命题
时命题 不成立,则
不成立,则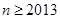 时命题
时命题 不成立;
不成立;
(2)当 时命题
时命题 不成立,则
不成立,则 时命题
时命题 不成立;
不成立;
(3)当 时命题
时命题 成立,则
成立,则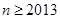 时命题
时命题 成立;
成立;
(4)当 时命题
时命题 成立,则
成立,则 时命题
时命题 成立.
成立.
其中正确判断的序号是 .(写出所有正确判断的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com