
【题目】设函数f(x)= ![]() ,关于x的方程[f(x)]2+mf(x)﹣1=0有三个不同的实数解,则实数m的取值范围是( )
,关于x的方程[f(x)]2+mf(x)﹣1=0有三个不同的实数解,则实数m的取值范围是( )
A.(﹣∞,e﹣ ![]() )
)
B.(e﹣ ![]() ,+∞)
,+∞)
C.(0,e)
D.(1,e)
【答案】B
【解析】解:f′(x)= ![]() , ∴当x>e时,f′(x)<0,当0<x<e时,f′(x)>0,
, ∴当x>e时,f′(x)<0,当0<x<e时,f′(x)>0,
∴f(x)在(0,e]上单调递增,在(e,+∞)上单调递减.
∴fmax(x)=f(e)= ![]() .
.
作出f(x)的大致函数图象如下: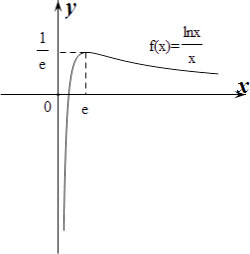
由图象可知当0<k ![]() 时,f(x)=k有两解,
时,f(x)=k有两解,
当k≤0或k= ![]() 时,f(x)=k有一解,当k
时,f(x)=k有一解,当k ![]() 时,f(x)=k无解.
时,f(x)=k无解.
令g(x)=x2+mx﹣1,则g(f(x))有三个零点,
∴g(x)在(0, ![]() )上有一个零点,在(﹣∞,0]∪{
)上有一个零点,在(﹣∞,0]∪{ ![]() }上有一个零点.
}上有一个零点.
∵g(x)的图象开口向上,且g(0)=﹣1,∴g(x)在(﹣∞,0)上必有一个零点,
∴g( ![]() )>0,即
)>0,即 ![]() ,
,
解得m>e﹣ ![]() .
.
故选B.
求出f(x)的单调性和极值,判断方程f(x)=k的根的情况,令g(x)=x2+mx﹣1,根据f(x)=k的根的情况得出g(x)的零点分布情况,利用零点的存在性定理列出不等式求出m的范围.


科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项和,a1=1,Sn=2Sn﹣1+n﹣2(n≥2),则a2017等于( )
A.22016﹣1
B.22016+1
C.22017﹣1
D.22017+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:kx﹣y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线l不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)(x∈R)的图象如图所示,f′(x)是f(x)的导函数,则不等式(x﹣1)f′(x)<0的解集为( ) 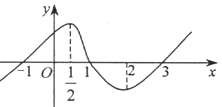
A.(﹣∞, ![]() )∪(1,2)
)∪(1,2)
B.(﹣1,1)∪(1,3)
C.(﹣1, ![]() )∪(3,+∞)
)∪(3,+∞)
D.(﹣∞,﹣1)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是各项为正数的等比数列,{bn}是等差数列,且a1=b1=1,b2+b3=2a3 , a5﹣3b2=7.
(1)求{an}和{bn}的通项公式;
(2)设cn=anbn , n∈N* , 求数列{cn}的前n项和为Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题: 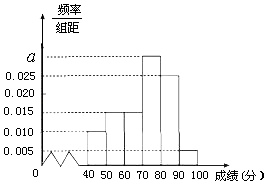
(1)求a并估计这次考试中该学科的中位数、平均值;
(2)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组…第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差不小于30分(以分数段为依据,不以具体学生分数为依据,如:[40,50),[70,80)这两组分数之差为30分),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线的方程;
(2)从圆C外一点P(x1 , y1)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是计算1 ![]() 的值的程序框图,则图中①、②处应填写的语句分别是( )
的值的程序框图,则图中①、②处应填写的语句分别是( )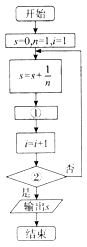
A.n=n+2,i>10?
B.n=n+2,i≥10?
C.n=n+1,i>10?
D.n=n+1,i≥10?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(2,2),B(3,4),C(m,0),△ABC的面积为5.
(1)求m的值;
(2)若m>0,∠BAC的平分线交线段BC于D,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com