
【题目】在三棱柱![]() 中,
中,![]() 与
与![]() 均为等边三角形,
均为等边三角形,![]()
![]() ,O为BC的中点.
,O为BC的中点.
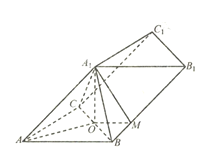
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)在棱![]() 上确定一点M,使得二面角
上确定一点M,使得二面角![]() 的大小为
的大小为![]() .
.
【答案】(1)见解析(2)![]()
【解析】
(1)要证明平面![]() 平面ABC,只需证明
平面ABC,只需证明![]() 平面ABC即可.因为
平面ABC即可.因为![]() 为等边三角形,所以
为等边三角形,所以![]() 再根据勾股定理证明
再根据勾股定理证明![]() ,即可证出
,即可证出![]() 平面ABC;
平面ABC;
(2)以OA,OB,![]() 所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系O-xyz,根据向量共线定理用参数
所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系O-xyz,根据向量共线定理用参数![]() 表示出点
表示出点![]() 的坐标,分别求出平面
的坐标,分别求出平面![]() 和平面
和平面![]() 的法向量,由二面角的向量公式列式,即可求出参数
的法向量,由二面角的向量公式列式,即可求出参数![]() ,确定
,确定![]() 的位置.
的位置.
(1)因为![]() 与
与![]() 均为等边三角形,
均为等边三角形,![]() ,O为BC的中点,
,O为BC的中点,
所以![]()
![]() .
.
在![]() 中,
中,![]()
![]() ,
,
从而有![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面ABC,
平面ABC,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面ABC.
平面ABC.
(2)以OA,OB,![]() 所在直线分别为x轴,y轴,z轴
所在直线分别为x轴,y轴,z轴
建立如图所示的空间直角坐标系O-xyz,
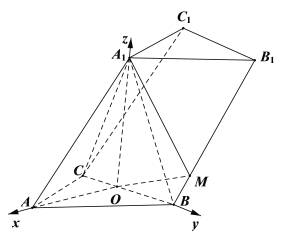
则![]()
![]()
![]()
![]() ,
,
![]() ,由(1)可知,
,由(1)可知,![]() 平面
平面![]() ,
,
![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设![]() ,其中
,其中![]() .
.
所以![]()
![]()
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则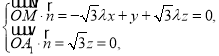
取![]() ,则
,则![]() ,
,
所以![]()
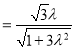
![]() ,
,
解得![]() .
.
即存在一点M,且![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.


科目:高中数学 来源: 题型:
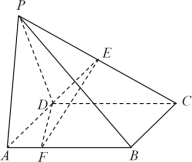
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,且
是正方形,且![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)设二面角![]() 的平面角为
的平面角为![]() ,试判断在线段
,试判断在线段![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整,调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额,依照个人所得税税率表,调整前后的计算方法如下表:

(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:

①先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用
的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,
元的人数,![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,随机变量
元的人数,随机变量![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
②小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
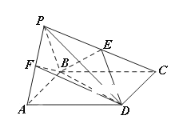
【题目】如图,四棱锥![]() 中,
中,![]() 是正三角形,四边形ABCD是矩形,且平面
是正三角形,四边形ABCD是矩形,且平面![]() 平面
平面![]() .
.
(1)若点E是PC的中点,求证:![]() 平面BDE;
平面BDE;
(2)若点F在线段PA上,且![]() ,当三棱锥
,当三棱锥![]() 的体积为
的体积为![]() 时,求实数
时,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行象棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)用X表示比赛决出胜负时的总局数,求随机变量X的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com