
 的定义域为D,若存在闭区间[a,b]
的定义域为D,若存在闭区间[a,b] D,使得函数
D,使得函数 满足:(1)
满足:(1) 在[a,b]内是单调函数;(2)
在[a,b]内是单调函数;(2) 在[a,b]上的值域为[2a,2b],则称区间[a,b]为y=
在[a,b]上的值域为[2a,2b],则称区间[a,b]为y= 的“美丽区间”.下列函数中存在“美丽区间”的是 . (只需填符合题意的函数序号)
的“美丽区间”.下列函数中存在“美丽区间”的是 . (只需填符合题意的函数序号)  ; ②、
; ②、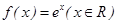 ;
; ; ④、
; ④、 .
. 在[a,b]内是单调增函数;
在[a,b]内是单调增函数; ,解得
,解得 ∴f(x)=x2(x≥0),若存在“美丽区间”[0,2],∴f(x)=x2(x≥0),若存在“美丽区间”[0,2];②f(x)=ex(x∈R),若存在“美丽区间”[a,b],则
∴f(x)=x2(x≥0),若存在“美丽区间”[0,2],∴f(x)=x2(x≥0),若存在“美丽区间”[0,2];②f(x)=ex(x∈R),若存在“美丽区间”[a,b],则 ,所以
,所以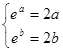 ,构建函数g(x)=ex-2x,∴g′(x)=ex-2,∴函数在(-∞,ln2)上单调减,在(ln2,+∞)上单调增,∴函数在x=ln2处取得极小值,且为最小值.∵g(ln2)=2-2ln2>0,∴g(x)>0恒成立,∴ex-2x=0无解,故函数不存在“美丽区间”;③
,构建函数g(x)=ex-2x,∴g′(x)=ex-2,∴函数在(-∞,ln2)上单调减,在(ln2,+∞)上单调增,∴函数在x=ln2处取得极小值,且为最小值.∵g(ln2)=2-2ln2>0,∴g(x)>0恒成立,∴ex-2x=0无解,故函数不存在“美丽区间”;③ 在
在 上单调递减,若存在“美丽区间”[a,b],则
上单调递减,若存在“美丽区间”[a,b],则 ,则
,则 ,故存在;④
,故存在;④ ,
, ,若存在“倍值区间”[a,b]⊆[0,1],则
,若存在“倍值区间”[a,b]⊆[0,1],则 ∴a=0,b=1,若存在“美丽区间”[0,1];故存在“美丽区间”的是①③④.
∴a=0,b=1,若存在“美丽区间”[0,1];故存在“美丽区间”的是①③④.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在 段可近似地用解析式
段可近似地用解析式 来描述,从
来描述,从 点走到今天的
点走到今天的 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且 点和
点和 点正好关于直线
点正好关于直线 :
: 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里 段与
段与 段关于直线
段关于直线 对称,
对称, 段是股价延续
段是股价延续 段的趋势(规律)走到这波上升行
段的趋势(规律)走到这波上升行
 。现在老张决定取点
。现在老张决定取点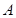
 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,
,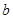 ,
, ,
, ,并且求得
,并且求得 。
。 ,
,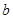 ,
, ,并回答股价什么时候见顶(即求
,并回答股价什么时候见顶(即求 点的横坐标)
点的横坐标) 点处的价格买入该股票3000股,到见顶处
点处的价格买入该股票3000股,到见顶处 点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
点的价格全部卖出,不计其它费用,这次操作他能赚多少元?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com