���𰸡�
��������1���������
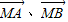
�����꣬�Ӷ��õ�
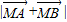
����x��y�ı���ʽ���������е�ʽ�������ã�
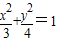
����Ϊ��������C�ķ��̣�
��2����P��x��y����M��x
��y
����N��-x
��-y
������M��N����ֱ���루1�����������Բ���̣���������������ɵ�
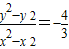
���ɴ˻���k
PM•k
PN����k
PM•k
PN��ֵ�����-

�����P��λ�ú�ֱ��L��λ���أ�
��3����P��x��y��������Բ���̣��ɵ�x
2=3-

y
2��-2��y��2���ɴ˻����|
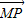
|=
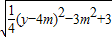
����Ϊ����P������Ϊ��0��2��ʱ
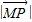
ȡ����С�����Խ�϶��κ��������ʵ�4m��2����֮��
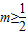
�������-2��y��2�����ɵõ�ʵ��m��ȡֵ��Χ��
����⣺��1�������⣬�ɵ�
��A��-1��1����B��1��1����M��x��y��
��
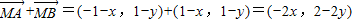
��
�ɴ˿ɵã�
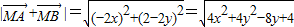
��
�֡�
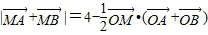
����
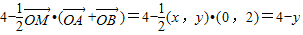
��
��
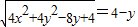
��
���������ã�
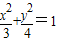
����Ϊ��������C�ķ��̣�
��2����Ϊ��ԭ���ֱ��L����Բ�ཻ������M��N��������ԭ��Գƣ�
���Կ���P��x��y����M��x
��y
����N��-x
��-y
����
��P��M��N����Բ�ϣ�
��
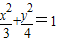
�����٣�
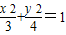
������
��-�ڣ���
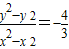
��
�֡�
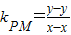
��
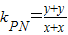
��
��
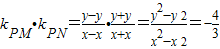
��
��ˣ�k
PM•k
PN��ֵ�����-

�����P��λ�ú�ֱ��L��λ���أ�
��3������P��x��y������ԲC��
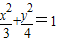
���˶����ɵ�x
2=3-

y
2��-2��y��2
��
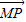
=��x��y-m����
��|
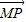
|=
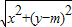
=
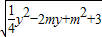
=
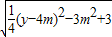
�����⣬��P������Ϊ��0��2��ʱ��
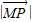
ȡ����Сֵ��
����y=2ʱ��
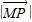
ȡ����Сֵ����-2��y��2������4m��2����֮��
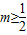
��
�֡���ԲC��y�ύ��D��E���������Ϊ��0��2������0��-2��������M���߶�DE�ϣ���-2��m��2��
��
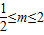
��ʵ��m��ȡֵ��Χ��
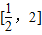
��
�����������������C�ϵĶ��������������ʽ��������C�ķ��̲�����б��֮��Ϊ��ֵ�����⣬���ؿ����˹켣���̵�����Բ�ļ������ʡ�ֱ������Բλ�ù�ϵ�������������������֪ʶ�������е��⣮

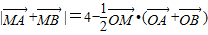 ��
��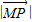 ȡ����Сֵ����ʵ��m��ȡֵ��Χ��
ȡ����Сֵ����ʵ��m��ȡֵ��Χ��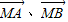 �����꣬�Ӷ��õ�
�����꣬�Ӷ��õ�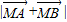 ����x��y�ı���ʽ���������е�ʽ�������ã�
����x��y�ı���ʽ���������е�ʽ�������ã�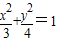 ����Ϊ��������C�ķ��̣�
����Ϊ��������C�ķ��̣�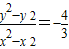 ���ɴ˻���kPM•kPN����kPM•kPN��ֵ�����-
���ɴ˻���kPM•kPN����kPM•kPN��ֵ�����- �����P��λ�ú�ֱ��L��λ���أ�
�����P��λ�ú�ֱ��L��λ���أ� y2��-2��y��2���ɴ˻����|
y2��-2��y��2���ɴ˻����|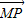 |=
|=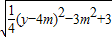 ����Ϊ����P������Ϊ��0��2��ʱ
����Ϊ����P������Ϊ��0��2��ʱ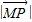 ȡ����С�����Խ�϶��κ��������ʵ�4m��2����֮��
ȡ����С�����Խ�϶��κ��������ʵ�4m��2����֮��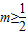 �������-2��y��2�����ɵõ�ʵ��m��ȡֵ��Χ��
�������-2��y��2�����ɵõ�ʵ��m��ȡֵ��Χ��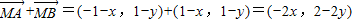 ��
��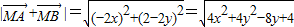 ��
��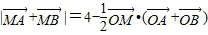 ����
����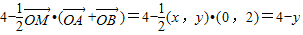 ��
��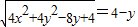 ��
��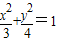 ����Ϊ��������C�ķ��̣�
����Ϊ��������C�ķ��̣�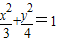 �����٣�
�����٣�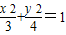 ������
������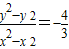 ��
��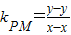 ��
��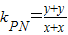 ��
��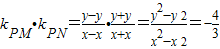 ��
�� �����P��λ�ú�ֱ��L��λ���أ�
�����P��λ�ú�ֱ��L��λ���أ�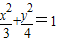 ���˶����ɵ�x2=3-
���˶����ɵ�x2=3- y2��-2��y��2
y2��-2��y��2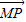 =��x��y-m����
=��x��y-m����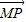 |=
|=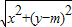 =
=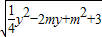 =
=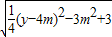
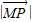 ȡ����Сֵ��
ȡ����Сֵ��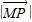 ȡ����Сֵ����-2��y��2������4m��2����֮��
ȡ����Сֵ����-2��y��2������4m��2����֮��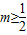 ��
��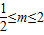 ��ʵ��m��ȡֵ��Χ��
��ʵ��m��ȡֵ��Χ��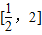 ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
 ��ͼ����ƽ��ֱ������ϵxOy�У���Ǧ��Ͷ۽Ǧµ��ձ߷ֱ��뵥λԲ����A��B���㣮����A�ĺ�������
��ͼ����ƽ��ֱ������ϵxOy�У���Ǧ��Ͷ۽Ǧµ��ձ߷ֱ��뵥λԲ����A��B���㣮����A�ĺ�������