练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知一个三边分别为15、19、23单位长度的三角形，若把它的三边分别缩短x单位长度且构成钝角三角形，试用不等式写出x的不等关系．

    答案：
    解析：

    解：缩短x单位长度后三边长分别为15－x，19－x，23－x，要使新的三角形是钝角三角形，则


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

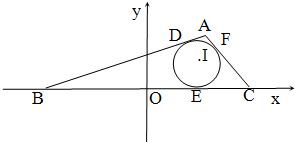    精英家教网如图，△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F，已知B（-
    		2
    ，0)    ，C(
    		2
    ，0)    ，内切圆圆心I（1，t）．设A点的轨迹为L
    （1）求L的方程；
    （2）过点C作直线m交曲线L于不同的两点M、N，问在x轴上是否存在一个异于点C的定点Q．使
    QM
    •
    QC
    |
    QM
    |
    =
    QN
    •
    QC
    |
    QN
    |
    对任意的直线m都成立？若存在，求出Q的坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•上海）已知抛物线F：y2=4x
    （1）△ABC的三个顶点在抛物线F上，记△ABC的三边AB、BC、CA所在的直线的斜率分别为kAB，kBC，kCA，若A的坐标在原点，求kAB-kBC+kCA的值；
    （2）请你给出一个以P（2，1）为顶点、其余各顶点均为抛物线F上的动点的多边形，写出各多边形各边所在的直线斜率之间的关系式，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2014届浙江省高一下期中理科数学试卷（解析版） 题型：解答题

    （本题满分15分）已知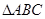的三边长分别为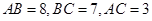，以点为圆心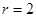，为半径作一个圆.

    (1) 求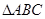的面积；

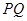    （2）设为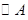的任意一条直径，记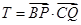,求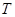的最大值和最小值，并说明当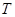取最大值和最小值时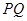，的位置特征是什么？

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年上海市普通高等学校高三春季招生数学卷 题型：解答题

    （本题满分14分）已知抛物线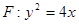

    （1）△ABC的三个顶点在抛物线F上，记△ABC的三边AB、BC、CA所在的直线的斜率分别为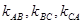，若A的坐标在原点，求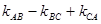的值；

    （2）请你给出一个以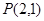为顶点、其余各顶点均为抛物线F上的动点的多边形，写出各多边形各边所在的直线斜率之间的关系式，并说明理由

     

    查看答案和解析>>

    科目：高中数学 来源：2011年上海市春季高考数学试卷（解析版） 题型：解答题

    已知抛物线F：y2=4x
    （1）△ABC的三个顶点在抛物线F上，记△ABC的三边AB、BC、CA所在的直线的斜率分别为kAB，kBC，kCA，若A的坐标在原点，求kAB-kBC+kCA的值；
    （2）请你给出一个以P（2，1）为顶点、其余各顶点均为抛物线F上的动点的多边形，写出各多边形各边所在的直线斜率之间的关系式，并说明理由．

    查看答案和解析>>

    同步练习册答案