
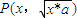 �Ĺ켣C�ķ��̣�
�Ĺ켣C�ķ��̣�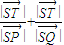 ��ȡֵ��Χ��
��ȡֵ��Χ��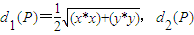 =
= �����ڣ�1���еĹ켣C���ڲ�ͬ������A1��A2��ʹ��d1��Ai��=
�����ڣ�1���еĹ켣C���ڲ�ͬ������A1��A2��ʹ��d1��Ai��=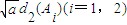 ��������ʵ��a��ȡֵ��Χ��
��������ʵ��a��ȡֵ��Χ��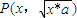 �Ĺ켣C�ķ��̼�
�Ĺ켣C�ķ��̼�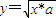 �����붨������㣬���ɵù켣C�ķ���
�����붨������㣬���ɵù켣C�ķ���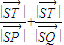
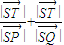 ��m�ĺ�����ϵ����Χ����
��m�ĺ�����ϵ����Χ����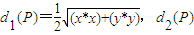 =
=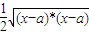 ���ֱ����
���ֱ����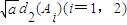 ��������ת��Ϊ����
��������ת��Ϊ����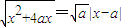 ��x��[0��+�ޣ����������ȵ�ʵ���⣬����Τ�ﶨ���õ�����ʽ�飬�������ʵ��a��ȡֵ��Χ
��x��[0��+�ޣ����������ȵ�ʵ���⣬����Τ�ﶨ���õ�����ʽ�飬�������ʵ��a��ȡֵ��Χ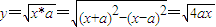 �ද��P�Ĺ켣C�ķ���Ϊ��y2=4ax��y��0��
�ද��P�Ĺ켣C�ķ���Ϊ��y2=4ax��y��0��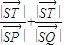 =
=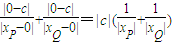 �������c��0��xP��0��xQ��0��
�������c��0��xP��0��xQ��0��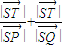 =
=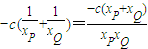
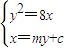 ��ȥy��x2-��2c+8m2��x+c2=0
��ȥy��x2-��2c+8m2��x+c2=0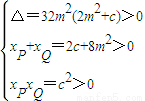 ��c��0����
��c��0����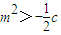 ��
��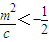 ��
��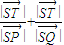 =
=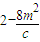 ��2��
��2��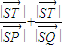 ��ȡֵ��Χ�ǣ�2��+�ޣ�
��ȡֵ��Χ�ǣ�2��+�ޣ�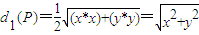 ��d2��P��=|x-a|
��d2��P��=|x-a|
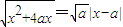 ��x��[0��+�ޣ����������ȵ�ʵ����
��x��[0��+�ޣ����������ȵ�ʵ����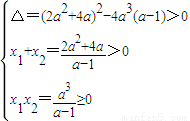


 ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x*a |
| A��Բ |
| B����Բ��һ���� |
| C��˫���ߵ�һ���� |
| D�������ߵ�һ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| y1?y2 |
| (x��a)-(x?a) |
| 1 |
| 2 |
| (x1?x2)+(y1?y2) |
| 15 |
| |d(ST)| |
| |d(SP)| |
| |d(ST)| |
| |d(SQ)| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| (x��a)-(x?a) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x*a |
|
| ||
|
|
|
| ||
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x*a |
|
| ||
|
|
|
| ||
|
|
| 1 |
| 2 |
| (x*x)+(y*y) |
| 1 |
| 2 |
| (x-a)*(x-a) |
| a |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com