Question

已知实数x，y满足2x+y≥1，则u=x²+y²+4x-2y的最小值为

-

9

5

．

Answer 1

分析：根据题意，设点P（x，y），它在区域2x+y≥1内运动，u表示点P（x，y）与定点A（-2，1）的距离的平方与5的差，问题转化为求定点A（-2，1）到由2x+y≥1所确定的平面区域的最近距离，故A到直线l的距离为A到区域G上点的距离的最小值，由此结合点到直线l的距离公式，即可得到u的最小值．

解答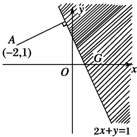：解析：由u=x²+y²+4x-2y=（x+2）²+（y-1）²-5
知，u表示点P（x，y）与定点A（-2，1）的距离的平方与5的差．
又由约束条件2x+y≥1知：
点P（x，y）在直线l：2x+y=1上及其右上方．
问题转化为求定点A（-2，1）到由2x+y≥1所确定的平面区域的最近距离．
故A到直线l的距离为A到区域G上点的距离的最小值．
d=

|2×?-2?+1-1|

22+12

=

4

5

，
∴d²=

16

5

，
∴u_min=d²-5=-

9

5

．
故答案：-

9

5

点评：本题给出实数x、y满足一次关系式，求它们平方和的最小值，着重考查了坐标系内简单线性规划的应用和点到直线的距离公式等知识，属于基础题．