
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了50人就该城市共享单车的推行情况进行问卷调査,并将问卷中的这50人根据其满意度评分值(百分制)按照![]() 分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
组别 | 分组 | 频数 | 频率 |
第1组 |
| 8 | 0.16 |
第2组 |
|
| ▆ |
第3组 |
| 20 | 0.40 |
第4组 |
| ▆ | 0.08 |
第5组 |
| 2 |
|
合计 | ▆ | ▆ |
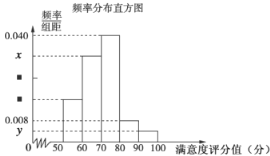
(1)求![]() 的值;
的值;
(2)若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据频率分布表可得b.先求得![]() 内的频数,即可由总数减去其余部分求得
内的频数,即可由总数减去其余部分求得![]() .结合频率分布直方图,即可求得
.结合频率分布直方图,即可求得![]() 的值.
的值.
(2)根据频率分布表可知在![]() 内有4人,在
内有4人,在![]() 有2人.列举出从这6人中选取2人的所有可能,由古典概型概率计算公式即可求解.
有2人.列举出从这6人中选取2人的所有可能,由古典概型概率计算公式即可求解.
(1)由频率分布表可得![]()
![]() 内的频数为
内的频数为![]() ,
,
∴![]()
∴![]() 内的频率为
内的频率为![]()
∴![]()
∵![]() 内的频率为0.04
内的频率为0.04
∴![]()
(2)由题意可知,第4组共有4人,第5组共有2人,
设第4组的4人分别为![]() 、
、![]() 、
、![]() 、
、![]() ;第5组的2人分别为
;第5组的2人分别为![]() 、
、![]()
从中任取2人的所有基本事件为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共15个.
共15个.
至少一人来自第5组的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 共9个.
共9个.
所以![]() .
.
∴所抽取2人中至少一人来自第5组的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,则以下四个命题:(1)
,则以下四个命题:(1)![]() 是等差数列;(2)
是等差数列;(2)![]() 中最大项是
中最大项是![]() ;(3)
;(3)![]() 通项公式是
通项公式是![]() ;(4)
;(4)![]() .其中真命题的序号是______.
.其中真命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点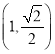 在椭圆上.
在椭圆上.
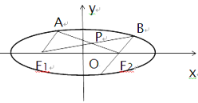
(1)求椭圆的方程;
(2)若A,B是椭圆上位于x轴上方的两点,直线![]() 与直线
与直线![]() 交于点P,
交于点P,![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 长轴的两个端点分别为
长轴的两个端点分别为![]() ,
,![]() , 离心率
, 离心率![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)作一条垂直于![]() 轴的直线,使之与椭圆
轴的直线,使之与椭圆![]() 在第一象限相交于点
在第一象限相交于点![]() ,在第四象限相交于点
,在第四象限相交于点![]() ,若直线
,若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,且直线
,且直线![]() 的斜率大于
的斜率大于![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分,众数,中位数;
(3)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如下表所示,求数学成绩在[50,90)之外的人数.
)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| 1:1 | 2:1 | 3:4 | 4:5 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com