
”¾ĢāÄæ”æ“ÓÄ³Ń§Š£øßȿ𼶹²![]() ĆūÄŠÉśÖŠĖ껜³éČ”
ĆūÄŠÉśÖŠĖ껜³éČ”![]() Ćū²āĮæÉķøߣ¬²āĮæ·¢ĻÖ±»²āѧɜÉķøßČ«²æ½éÓŚ
Ćū²āĮæÉķøߣ¬²āĮæ·¢ĻÖ±»²āѧɜÉķøßČ«²æ½éÓŚ![]() ŗĶ
ŗĶ![]() Ö®¼ä£¬½«²āĮæ½į¹ū°“ČēĻĀ·½Ź½·Ö³É°Ė×飬µŚŅ»×é
Ö®¼ä£¬½«²āĮæ½į¹ū°“ČēĻĀ·½Ź½·Ö³É°Ė×飬µŚŅ»×é![]() £»µŚ¶ž×é
£»µŚ¶ž×é![]() £¬
£¬![]() £¬µŚ°Ė×é
£¬µŚ°Ė×é![]() £¬ČēĶ¼ŹĒ°“ÉĻŹö·Ö×é·½·ØµĆµ½µÄʵĀŹ·Ö²¼Ö±·½Ķ¼µÄŅ»²æ·Ö£¬ČōµŚŅ»×éÓėµŚ°Ė×éČĖŹżĻąĶ¬£¬µŚĮł×锢µŚĘß×锢µŚ°Ė×éČĖŹżŅĄ“Ī¹¹³ÉµČ²īŹżĮŠ£®
£¬ČēĶ¼ŹĒ°“ÉĻŹö·Ö×é·½·ØµĆµ½µÄʵĀŹ·Ö²¼Ö±·½Ķ¼µÄŅ»²æ·Ö£¬ČōµŚŅ»×éÓėµŚ°Ė×éČĖŹżĻąĶ¬£¬µŚĮł×锢µŚĘß×锢µŚ°Ė×éČĖŹżŅĄ“Ī¹¹³ÉµČ²īŹżĮŠ£®

£Ø![]() £©¹Ą¼ĘÕāĖłŃ§Š£øßȿğ¼¶Č«ĢåÄŠÉśÉķøß
£©¹Ą¼ĘÕāĖłŃ§Š£øßȿğ¼¶Č«ĢåÄŠÉśÉķøß![]() ŅŌÉĻ£Øŗ¬
ŅŌÉĻ£Øŗ¬![]() £©µÄČĖŹż£®
£©µÄČĖŹż£®
£Ø![]() £©ĒóµŚĮł×锢µŚĘß×éµÄʵĀŹ²¢²¹³äĶźÕūʵĀŹ·Ö²¼Ö±·½Ķ¼£®£ØĒ¦±Ź×÷Ķ¼²¢ÓĆÖŠŠŌ±ŹĆčŗŚ£©£®
£©ĒóµŚĮł×锢µŚĘß×éµÄʵĀŹ²¢²¹³äĶźÕūʵĀŹ·Ö²¼Ö±·½Ķ¼£®£ØĒ¦±Ź×÷Ķ¼²¢ÓĆÖŠŠŌ±ŹĆčŗŚ£©£®
£Ø![]() £©Čō“ÓÉķøߏōÓŚµŚĮł×éŗĶµŚ°Ė×éµÄĖłÓŠÄŠÉśÖŠĖ껜³éČ”Į½ĆūÄŠÉś£¬¼ĒĖūĆĒµÄÉķøß·Ö±šĪŖ
£©Čō“ÓÉķøߏōÓŚµŚĮł×éŗĶµŚ°Ė×éµÄĖłÓŠÄŠÉśÖŠĖ껜³éČ”Į½ĆūÄŠÉś£¬¼ĒĖūĆĒµÄÉķøß·Ö±šĪŖ![]() ”¢
”¢![]() £¬ĒóĀś×ć
£¬ĒóĀś×ć![]() µÄŹĀ¼žøÅĀŹ£®
µÄŹĀ¼žøÅĀŹ£®
”¾“š°ø”æ£Ø1£©9ČĖ£»£Ø2£©¼ū½āĪö£»£Ø3£©![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼æɵĆĒ°Īå×éʵĀŹ£¬½ų¶ųæɵĆŗóČż×éʵĀŹŗĶČĖŹż£¬ÓÖæɵĆŗóČż×éµÄČĖŹż£¬æɵĆĘ½¾łÉķøߣ»
£Ø2£©Ņ×µĆŗóČż×éµÄ![]() £¬æɵĆʵĀŹ·Ö²¼Ö±·½Ķ¼£»
£¬æɵĆʵĀŹ·Ö²¼Ö±·½Ķ¼£»
£Ø3£©ÓÉ£Ø![]() £©ÖŖÉķøßŌŚ
£©ÖŖÉķøßŌŚ![]() ÄŚµÄČĖŹżĪŖ
ÄŚµÄČĖŹżĪŖ![]() ČĖ£¬
ČĖ£¬
Éč![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ”£ÉķøßĪŖ
”£ÉķøßĪŖ![]() µÄČĖŹżĪŖ
µÄČĖŹżĪŖ![]() ČĖ£¬
ČĖ£¬
ÉčĪŖ![]() £¬
£¬![]() £®£¬ĮŠ¾ŁæɵĆ×ܵĻł±¾ŹĀ¼ž¹²15ÖÖĒéæö£¬ŹĀ¼ž”°
£®£¬ĮŠ¾ŁæɵĆ×ܵĻł±¾ŹĀ¼ž¹²15ÖÖĒéæö£¬ŹĀ¼ž”°![]() ”±Ėł°üŗ¬µÄ»ł±¾ŹĀ¼žøöŹżÓŠ6+1=7£¬ÓÉøÅĀŹ¹«Ź½æÉµĆ£®
”±Ėł°üŗ¬µÄ»ł±¾ŹĀ¼žøöŹżÓŠ6+1=7£¬ÓÉøÅĀŹ¹«Ź½æÉµĆ£®
ŹŌĢā½āĪö£ŗ£Ø![]() £©ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼ÖŖ£¬
£©ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼ÖŖ£¬
Ē°Īå×éʵĀŹĪŖ![]() £¬
£¬
ŗóČż×éʵĀŹĪŖ![]() £¬ČĖŹżĪŖ
£¬ČĖŹżĪŖ![]() ČĖ£¬
ČĖ£¬
ÕāĖłŃ§Š£øßȿĊɜÉķøßŌŚ![]() ŅŌÉĻ£Øŗ¬
ŅŌÉĻ£Øŗ¬![]() £©µÄČĖŹżĪŖ
£©µÄČĖŹżĪŖ![]() ČĖ£®
ČĖ£®
£Ø![]() £©ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼µĆµŚ°Ė×éʵĀŹĪŖ
£©ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼µĆµŚ°Ė×éʵĀŹĪŖ![]() £¬ČĖŹżĪŖ
£¬ČĖŹżĪŖ![]() ČĖ£¬
ČĖ£¬
É赌Įł×éČĖŹżĪŖ![]() £¬ŌņµŚĘß×éČĖŹżĪŖ
£¬ŌņµŚĘß×éČĖŹżĪŖ![]() £¬ÓÖ
£¬ÓÖ![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() £¬
£¬
¼“µŚĮł×éČĖŹżĪŖ![]() ČĖ£¬µŚĘß×éČĖŹżĪŖ
ČĖ£¬µŚĘß×éČĖŹżĪŖ![]() ČĖ£¬ĘµĀŹ·Ö±šĪŖ
ČĖ£¬ĘµĀŹ·Ö±šĪŖ![]() £¬
£¬![]() £¬
£¬
ʵĀŹ³żŅŌ×é¾ą·Ö±šµČÓŚ![]() £¬
£¬![]() £¬¼ūĶ¼£®
£¬¼ūĶ¼£®
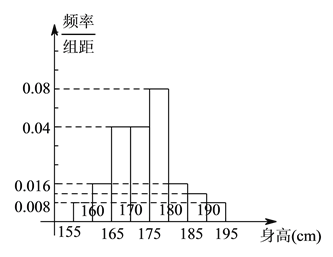
£Ø![]() £©ÓÉ£Ø
£©ÓÉ£Ø![]() £©ÖŖÉķøßŌŚ
£©ÖŖÉķøßŌŚ![]() ÄŚµÄČĖŹżĪŖ
ÄŚµÄČĖŹżĪŖ![]() ČĖ£¬
ČĖ£¬
Éč![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ”£ÉķøßĪŖ
”£ÉķøßĪŖ![]() µÄČĖŹżĪŖ
µÄČĖŹżĪŖ![]() ČĖ£¬
ČĖ£¬
ÉčĪŖ![]() £¬
£¬![]() £®
£®
Čō![]() £¬
£¬![]() Ź±£¬ÓŠ
Ź±£¬ÓŠ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ¹²ĮłÖÖĒéæö£®
¹²ĮłÖÖĒéæö£®
Čō![]() £¬
£¬![]() Ź±£¬ÓŠ
Ź±£¬ÓŠ![]() ¹²Ņ»ÖÖĒéæö£®
¹²Ņ»ÖÖĒéæö£®
Čō![]() £¬
£¬![]() ·Ö±šŌŚ
·Ö±šŌŚ![]() £¬
£¬![]() ÄŚŹ±£¬
ÄŚŹ±£¬
ÓŠ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ¹²
¹²![]() ÖÖĒéæö£®
ÖÖĒéæö£®
ĖłŅŌ»ł±¾ŹĀ¼žµÄ×ÜŹżĪŖ![]() ÖÖ£®
ÖÖ£®
ŹĀ¼ž![]() Ėł°üŗ¬µÄ»ł±¾ŹĀ¼žøöŹżÓŠ
Ėł°üŗ¬µÄ»ł±¾ŹĀ¼žøöŹżÓŠ![]() ÖÖ£¬¹Ź
ÖÖ£¬¹Ź![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĖµ·Ø£ŗ¢Ł²Š²īæÉÓĆĄ“ÅŠ¶ĻÄ£ŠĶÄāŗĻµÄŠ§¹ū;
¢ŚÉčÓŠŅ»øö»Ų¹é·½³Ģ![]() £¬±äĮæxŌö¼ÓŅ»øöµ„Ī»Ź±£¬yĘ½¾łŌö¼Ó5øöµ„Ī»£»
£¬±äĮæxŌö¼ÓŅ»øöµ„Ī»Ź±£¬yĘ½¾łŌö¼Ó5øöµ„Ī»£»
¢ŪĻߊŌ»Ų¹é·½³Ģ![]() ±Ų¹ż
±Ų¹ż![]() £»
£»
¢ÜŌŚŅ»øö2”Į2ĮŠĮŖ±ķÖŠ£¬ÓɼĘĖćµĆ![]() =13.079£¬ŌņÓŠ99%µÄ°ŃĪÕČ·ČĻÕāĮ½øö±äĮæ¼äÓŠ¹ŲĻµ£ØĘäÖŠ
=13.079£¬ŌņÓŠ99%µÄ°ŃĪÕČ·ČĻÕāĮ½øö±äĮæ¼äÓŠ¹ŲĻµ£ØĘäÖŠ![]() £©£»
£©£»
ĘäÖŠ“ķĪóµÄøöŹżŹĒ£Ø £©
A. 0 B. 1 C. 2 D. 3.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£ĪŖĮĖ½āøßŅ»ŹµŃé°ąµÄŹżŃ§³É¼Ø,²ÉÓĆ³éŃłµ÷²éµÄ·½Ź½,»ńČ”ĮĖ![]() Ī»Ń§ÉśŌŚµŚŅ»Ń§ĘŚÄ©µÄŹżŃ§³É¼ØŹż¾Ż,Ńł±¾Ķ³¼Ę½į¹ūČēĻĀ±ķ£ŗ
Ī»Ń§ÉśŌŚµŚŅ»Ń§ĘŚÄ©µÄŹżŃ§³É¼ØŹż¾Ż,Ńł±¾Ķ³¼Ę½į¹ūČēĻĀ±ķ£ŗ
·Ö×é | ʵŹż | ʵĀŹ |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
ŗĻ¼Ę |
|
|
(1)Ēó![]() µÄÖµŗĶŹµŃé°ąŹżŃ§Ę½¾ł·ÖµÄ¹Ą¼ĘÖµ£»
µÄÖµŗĶŹµŃé°ąŹżŃ§Ę½¾ł·ÖµÄ¹Ą¼ĘÖµ£»
(2)Čē¹ūÓĆ·Ö²ć³éŃłµÄ·½·Ø“ÓŹżŃ§³É¼ØŠ”ÓŚ![]() ·ÖµÄѧɜ֊³éČ”
·ÖµÄѧɜ֊³éČ”![]() Ćūѧɜ,ŌŁ“ÓÕā
Ćūѧɜ,ŌŁ“ÓÕā![]() Ćūѧɜ֊є
Ćūѧɜ֊є![]() ČĖ,ĒóÖĮÉŁÓŠŅ»øöѧɜµÄŹżŃ§³É¼ØŹĒŌŚ
ČĖ,ĒóÖĮÉŁÓŠŅ»øöѧɜµÄŹżŃ§³É¼ØŹĒŌŚ![]() µÄøÅĀŹ.
µÄøÅĀŹ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() .
.
(1)Ēóf(2)£¬f(x)£»
(2)Ö¤Ć÷£ŗŗÆŹżf(x)ŌŚ[1£¬17]ÉĻĪŖŌöŗÆŹż£»
(3)ŹŌĒóŗÆŹżf(x)ŌŚ[1£¬17]ÉĻµÄ×ī“óÖµŗĶ×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹżf£Øx£©=![]() £Øx
£Øx![]() R£©£¬g£Øx£©=2a-1
R£©£¬g£Øx£©=2a-1
£Ø1£©ĒóŗÆŹżf£Øx£©µÄµ„µ÷Ēų¼äÓė¼«Öµ£®
£Ø2£©Čōf£Øx£©”Żg£Øx£©¶Ō![]() ŗć³ÉĮ¢£¬Ē󏵏żaµÄȔֵ·¶Ī§.
ŗć³ÉĮ¢£¬Ē󏵏żaµÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉčĄėŠÄĀŹĪŖ ![]() µÄĶÖŌ²E£ŗ
µÄĶÖŌ²E£ŗ ![]() +
+ ![]() =1£Øa£¾b£¾0£©µÄ×ó”¢ÓŅ½¹µćĪŖF1 £¬ F2 £¬ µćPŹĒEÉĻŅ»µć£¬PF1”ĶPF2 £¬ ”÷PF1F2ÄŚĒŠŌ²µÄ°ė¾¶ĪŖ
=1£Øa£¾b£¾0£©µÄ×ó”¢ÓŅ½¹µćĪŖF1 £¬ F2 £¬ µćPŹĒEÉĻŅ»µć£¬PF1”ĶPF2 £¬ ”÷PF1F2ÄŚĒŠŌ²µÄ°ė¾¶ĪŖ ![]() ©1£®
©1£®
£Ø1£©ĒóEµÄ·½³Ģ£»
£Ø2£©¾ŲŠĪABCDµÄĮ½¶„µćC”¢DŌŚÖ±Ļßy=x+2£¬A”¢BŌŚĶÖŌ²EÉĻ£¬Čō¾ŲŠĪABCDµÄÖܳ¤ĪŖ ![]() £¬ĒóÖ±ĻßABµÄ·½³Ģ£®
£¬ĒóÖ±ĻßABµÄ·½³Ģ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓĆæÕ¼äĻņĮæ½ā¾öĻĀĮŠĪŹĢā£ŗČēĶ¼£¬ŌŚŠ±ČżĄāÖł![]() ÖŠ£¬
ÖŠ£¬ ![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬
µÄÖŠµć£¬ ![]() ”ĶĘ½Ćę
”ĶĘ½Ćę![]() £¬
£¬ ![]() £¬
£¬ ![]() £®
£®

£Ø1£©ĒóÖ¤£ŗ ![]() £»
£»
£Ø2£©Ēó¶žĆę½Ē![]() µÄÓąĻŅÖµ£®
µÄÓąĻŅÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĶÖŌ²C£ŗ ![]() µÄĄėŠÄĀŹĪŖ
µÄĄėŠÄĀŹĪŖ ![]() £¬ÓŅ½¹µćĪŖF£¬µćB£Ø0£¬1£©ŌŚĶÖŌ²CÉĻ£®
£¬ÓŅ½¹µćĪŖF£¬µćB£Ø0£¬1£©ŌŚĶÖŌ²CÉĻ£®
£Ø¢ń£©ĒóĶÖŌ²CµÄ·½³Ģ£»
£Ø¢ņ£©¹żµć ![]() µÄÖ±Ļß½»ĶÖŌ²CÓŚM£¬NĮ½µć£¬½»Ö±Ļßx=2ÓŚµćP£¬Éč
µÄÖ±Ļß½»ĶÖŌ²CÓŚM£¬NĮ½µć£¬½»Ö±Ļßx=2ÓŚµćP£¬Éč ![]() £¬
£¬ ![]() £¬ĒóÖ¤£ŗ¦Ė+¦ĢĪŖ¶ØÖµ£®
£¬ĒóÖ¤£ŗ¦Ė+¦ĢĪŖ¶ØÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ČżĄā׶A£BCDÖŠ£¬AB”ĶĘ½ĆęBCD£¬CD”ĶBD .

£Ø1£©ĒóÖ¤£ŗCD”ĶĘ½ĆęABD£»
£Ø2£©ČōAB£½BD£½CD£½1£¬MĪŖADÖŠµć£¬ĒóČżĄā׶A£MBCµÄĢå»ż£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com