
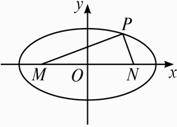
解析:题中没有给出坐标系,我们根据图形的对称性,建立坐标系.当然,我们可以尝试建立其他的坐标系.?
在此题中,角的正切可看作相应直线的斜率,从而得点P的坐标与c的关系,求a时可有三种方法:代入点法,利用椭圆的第一定义得方程;利用点在椭圆上,将点的坐标代入椭圆方程;根据△PMN是直角三角形.我们这里只介绍一种方法,读者可自己尝试其他方法.?

解:如图,以MN所在直线为x轴,MN的垂直平分线为y轴建立坐标系.?
设以M、N为焦点,且过点P的椭圆方程为![]() =1,焦点为M(-c,0),N(c,0).?
=1,焦点为M(-c,0),N(c,0).?
由tan∠PMN=![]() ,tan∠PNx=tan(π-∠PNM)=-2,
,tan∠PNx=tan(π-∠PNM)=-2,
得直线PM和PN的方程分别为y=![]() (x+c)和y=-2(x-c),?
(x+c)和y=-2(x-c),?
联立两方程解得x=![]() c,y=
c,y=![]() c,?
c,?
即P点坐标为(![]() c,
c,![]() c).?
c).?
在△PMN中,MN=2c,MN上的高为![]() c,?
c,?
∴S△MNP=12×2c×45c=1.?
∴c=![]() ,即P点坐标为(
,即P点坐标为(![]() ),?
),?
|PM|=![]() =2,|PN|=
=2,|PN|=![]() =1.?
=1.?
∴a=![]() (|PM|+|PN|)=
(|PM|+|PN|)=![]() .从而b2=a2-c2=1,故所求椭圆方程为
.从而b2=a2-c2=1,故所求椭圆方程为![]() x2+y2=1.
x2+y2=1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,在面积为1的正△A1B1C1内作正△A2B2C2,使
如图,在面积为1的正△A1B1C1内作正△A2B2C2,使| A1A2 |
| A2B1 |
| B1B2 |
| B2C1 |
| C1C2 |
| C2A1 |
| 3 |
| 2 |
| 1 |
| 3n |
| 3 |
| 2 |
| 1 |
| 3n |
查看答案和解析>>
科目:高中数学 来源:2014届广东省实验学校高一下期中理科数学试卷(解析版) 题型:填空题
如图,在面积为1的正 内作正
内作正 ,使
,使 ,
,  ,
, ,依此类推,
在正
,依此类推,
在正 内再作正
内再作正 ,……。记正
,……。记正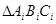 的面积为
的面积为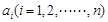 ,则a1+a2+……+an= _________
,则a1+a2+……+an= _________

查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省高二上学期第三次阶段性测试理科数学卷 题型:填空题
如图,在面积为1的正 内作正
内作正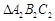 ,使
,使 ,
, ,
, ,依此类推,
在正
,依此类推,
在正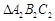 内再作正
内再作正 ,……。记正
,……。记正 的面积为
的面积为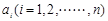 ,则a1+a2+……+an=
。
,则a1+a2+……+an=
。

查看答案和解析>>
科目:高中数学 来源:2010年江西省九江市高二第一次阶段测试理科数学试卷 题型:填空题
如图,在面积为1的正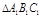 内作正
内作正 ,使
,使 ,
,
 ,
,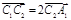 ,依此类推,
在正
,依此类推,
在正 内再作正
内再作正 ,……。记正
,……。记正 的面积为
的面积为 ,则a1+a2+……+an= 。
,则a1+a2+……+an= 。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省汕头市金山中学高二(上)期中数学试卷(理科)(解析版) 题型:填空题
 ,
, ,
, ,依此类推,在正△A2B2C2内再作正△A3B3C3,….记正△AiBiCi的面积为ai(i=1,2,…,n),则a1+a2+…+an= .
,依此类推,在正△A2B2C2内再作正△A3B3C3,….记正△AiBiCi的面积为ai(i=1,2,…,n),则a1+a2+…+an= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com