
本小题满分12分)已知实数 ,
,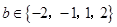 .
.
(Ⅰ)求点(a,b)在第一象限的概率;
(Ⅱ)求直线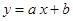 与圆
与圆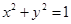 有公共点的概率.
有公共点的概率.
解:由于实数对 的所有取值为:
的所有取值为: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,共16种.
,共16种.
设“点(a,b)在第一象限”为事件 ,“直线
,“直线 与圆
与圆 有公共点”为事件
有公共点”为事件 .
.
(1)若点(a,b)在第一象限,则必须满足
即满足条件的实数对 有
有 ,
, ,
, ,
, ,共4种.
,共4种.
∴ ,故直线
,故直线 不经过第四象限的概率为
不经过第四象限的概率为 .
.
(2)若直线 与圆
与圆 有公共点,则必须满足
有公共点,则必须满足 ≤1,即
≤1,即 ≤
≤ .
.
若 ,则
,则 符合要求,此时实数对(
符合要求,此时实数对( )有4种不同取值;
)有4种不同取值;
若 ,则
,则 符合要求,此时实数对(
符合要求,此时实数对( )有2种不同取值;
)有2种不同取值;
若 ,则
,则 符合要求,此时实数对(
符合要求,此时实数对( )有2种不同取值;
)有2种不同取值;
若 ,则
,则 符合要求,此时实数对(
符合要求,此时实数对( )有4种不同取值.∴满足条件的实数对
)有4种不同取值.∴满足条件的实数对 共有12种不同取值.∴
共有12种不同取值.∴ . 故直线
. 故直线 与圆
与圆 有公共点的概率为
有公共点的概率为 .
.
【解析】本试题主要是考查了古典概型概率的公式的运用。
(1)因为分析试验的基本事件空间是解决问题的第一要素,然后进一步分析事件发生的基本事件数,结合概率公式得到。
(2)因为直线 与圆
与圆 有公共点,则必须满足
有公共点,则必须满足 ≤1,即
≤1,即 ≤
≤ .然后分析满足不等是的a,b的组合有多少,然后得到概率值。
.然后分析满足不等是的a,b的组合有多少,然后得到概率值。


科目:高中数学 来源:2010-2011学年辽宁省辽南协作体高一下学期期中考试数学(理) 题型:解答题
(本小题满分12分)
已知向量 ,记函数
,记函数 ,
,
若函数 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)当 时,试求
时,试求 的值域;
的值域;
(3)求 在
在 上的单调递增区间.
上的单调递增区间.
查看答案和解析>>
科目:高中数学 来源:2011届黑龙江省大庆实验中学高三高考仿真模拟试题理数 题型:解答题
((本小题满分12分)
已知椭圆
 是椭圆上纵坐标不为零的两点,若
是椭圆上纵坐标不为零的两点,若 其中F为椭圆的左焦点.
其中F为椭圆的左焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)求线段AB的垂直平分线在y轴上的截距的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011年江西省普通高中招生考试文科数学 题型:解答题
(本小题满分12分)
已知过抛物线 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于
 (
( )两点,且
)两点,且 .
.
(1)求该抛物线的方程;
(2) 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南灵宝第三高级中学高三上学期第三次质量检测文数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知条件 ,
,
条件 ,
,
(1)若 ,求实数
,求实数 的值;
的值;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省永年二中涉县一中临漳一中高三联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数 ,且对于任意实数
,且对于任意实数 ,恒有
,恒有 .
.
(1)求函数 的解析式;
的解析式;
(2)函数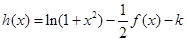 有几个零点?
有几个零点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com