
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆上.
在椭圆上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设动直线
)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() ,
, ![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 、
、![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
【答案】(1) 椭圆方程为![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(I)借助题设条件建立方程组求解;(II)借助题设运用直线与椭圆的位置关系推证和探求.
试题解析:
(I)由题意得: ![]() ,
, ![]() ,
,
又点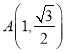 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,解得
,解得![]() ,
, ![]() ,
, ![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .………………5分
.………………5分
(II)存在符合条件的圆,且此圆的方程为![]() .
.
证明如下:假设存在符合条件的圆,并设此圆的方程为![]() .
.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() .
.
由方程组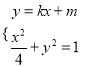 得
得![]() .
.
∵直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,
有且仅有一个公共点,
∴![]() ,即
,即![]() .
.
由方程组![]() 得
得![]() ,
,
则![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
设直线![]() 的斜率分别为
的斜率分别为![]() ,
,
∴![]()
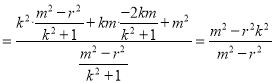 ,将
,将![]() 代入上式,
代入上式,
得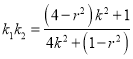 .
.
要使得![]() 为定值,则
为定值,则![]() ,即
,即![]() ,代入
,代入![]() 验证知符合题意.
验证知符合题意.
∴当圆的方程为![]() 时,圆与
时,圆与![]() 的交点
的交点![]() 满足
满足![]() 为定值
为定值![]() .
.
当直线![]() 的斜率不存在时,由题意知
的斜率不存在时,由题意知![]() 的方程为
的方程为![]() .
.
此时,圆![]() 与
与![]() 的交点
的交点![]() 也满足
也满足![]() .
.
综上,当圆的方程为![]() 时,
时,
圆与![]() 的交点
的交点![]() 满足直线
满足直线![]() 的斜率之积为定值
的斜率之积为定值![]() .……………………12分
.……………………12分


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为  (t为参数),在以坐标原点O为极点,x轴的正非负半轴为极轴,取相同单位长度的极坐标系中,圆的极坐标方程为ρ=4sinθ.
(t为参数),在以坐标原点O为极点,x轴的正非负半轴为极轴,取相同单位长度的极坐标系中,圆的极坐标方程为ρ=4sinθ.
(1)求直线l被圆截得的弦长;
(2)从极点作圆C的弦,求各弦中点的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3-3ax+b(a≠0).
(1)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调区间与极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如表:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计芯片甲,芯片乙为合格品的概率;
(2)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣4:坐标系与参数方程.
极坐标系与直角坐标系xoy有相同的长度单位,以原点为极点,以x轴正半轴为极轴,已知曲线C1的极坐标方程为ρ=4cosθ,曲线C2的参数方程为 ![]() (t为参数,0≤α<π),射线θ=φ,θ=φ+
(t为参数,0≤α<π),射线θ=φ,θ=φ+ ![]() ,θ=φ﹣
,θ=φ﹣ ![]() 与曲线C1交于(不包括极点O)三点A、B、C.
与曲线C1交于(不包括极点O)三点A、B、C.
(1)求证:|OB|+|OC|= ![]() |OA|;
|OA|;
(2)当φ= ![]() 时,B,C两点在曲线C2上,求m与α的值.
时,B,C两点在曲线C2上,求m与α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A-BCDE中,底面BCDE是等腰梯形,BC∥ DE,∠ DCB=45°,O是BC中点,AO=![]() ,且BC=6,AD=AE=2CD=
,且BC=6,AD=AE=2CD=![]() .
.
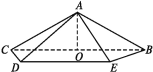
(1)证明:AO⊥平面BCD;
(2)求二面角A-CD-B的平面角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com