Question

【题目】已两动圆和，把它们的公共点的轨迹记为曲线，若曲线与轴的正半轴交点为，且曲线上异于点的相异两点、满足.

(1)求曲线的方程；

(2)证明直线恒经过一定点，并求出此定点的坐标.

Answer 1

【答案】（1）；（2）直线恒过定点。

【解析】

（1）设两动圆的公共点为，则有，运用椭圆的定义，即可得到，，，进而得到的轨迹方程；

（2），设，，，，根据直线的斜率不存在和存在，设出直线方程，根据条件，运用向量的数量积的坐标表示，结合韦达定理和直线恒过定点的求法，即可得到定点；

解：（1）设两动圆的公共点为，则有．

由椭圆的定义可知的轨迹是以、为焦点椭圆，且．，

所以曲线的方程是：．

（2）证明：由题意可知：，设，，，，

当的斜率不存在时，易知满足条件的直线为：，过定点；

当的斜率存在时，设直线，联立方程组：，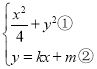

把②代入①有：，

③，④，

因为，所以有即，

，

把③④代入整理：，

（有公因式继续化简得，或（舍去，

综上，直线恒过定点．