
【题目】某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第x个月的利润  (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第x个月的当月利润率
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第x个月的当月利润率 ![]() ,例如:
,例如: ![]() .
.
(1)求g(10);
(2)求第x个月的当月利润率g(x);
(3)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
【答案】
(1)解:由题意得:f(1)=f(2)=f(3)=…═f(9)=f(10)=1
g(x)= ![]() =
= ![]() =
= ![]()
(2)解:当1≤x≤20时,f(1)=f(2)═f(x﹣1)=f(x)=1
∴g(x)= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
当21≤x≤60时,
g(x)= ![]()
= ![]()
= 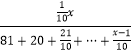
= 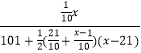
= 
∴当第x个月的当月利润率
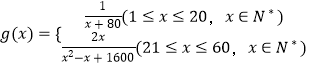
(3)解:当1≤x≤20时, ![]() 是减函数,
是减函数,
此时g(x)的最大值为 ![]()
当21≤x≤60时,
![]()
当且仅当 ![]() 时,即x=40时,
时,即x=40时,
![]() ,又∵
,又∵ ![]() ,
,
∴当x=40时, ![]()
所以,该企业经销此产品期间,第40个月的当月利润率最大,最大值为 ![]()
【解析】(1)当1≤x≤20时,f(x)=1,易知f(1)=f(2)=f(3)=…=f(9)=f(10)=1,从而知 ![]() (2)求第x个月的当月利润率,要考虑1≤x≤20,21≤x≤60时f(x)的值,代入
(2)求第x个月的当月利润率,要考虑1≤x≤20,21≤x≤60时f(x)的值,代入 ![]() 即可.(3)求那个月的当月利润率最大时,由(2)得出的分段函数,利用函数的单调性,基本不等式
即可.(3)求那个月的当月利润率最大时,由(2)得出的分段函数,利用函数的单调性,基本不等式 ![]() 可得,解答如下:
可得,解答如下:
【考点精析】关于本题考查的函数的最值及其几何意义,需要了解利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能得出正确答案.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx,g(x)=(2﹣a)(x﹣1)﹣2f(x). (Ⅰ)当a=1时,求函数g(x)的单调区间;
(Ⅱ)设F(x)=|f(x)|+ ![]() (b>0).对任意x1 , x2∈(0,2],x1≠x2 , 都有
(b>0).对任意x1 , x2∈(0,2],x1≠x2 , 都有 ![]() <﹣1,求实数b的取值范围.
<﹣1,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(2,﹣
=(2,﹣ ![]() ),
), ![]() =(sin2(
=(sin2( ![]() +x),cos2x).令f(x)=
+x),cos2x).令f(x)= ![]()
![]() ﹣1,x∈R,函数g(x)=f(x+φ),φ∈(0,
﹣1,x∈R,函数g(x)=f(x+φ),φ∈(0, ![]() )的图象关于(﹣
)的图象关于(﹣ ![]() ,0)对称. (Ⅰ) 求f(x)的解析式,并求φ的值;
,0)对称. (Ⅰ) 求f(x)的解析式,并求φ的值;
(Ⅱ)在△ABC中sinC+cosC=1﹣ ![]() ,求g(B)的取值范围.
,求g(B)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn是数列{an}的前n项和,已知a1=3,an+1=2Sn+3(n∈N) (I)求数列{an}的通项公式;
(Ⅱ)令bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
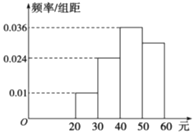
【题目】某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在![]() 元的学生有60人,则下列说法正确的是______.
元的学生有60人,则下列说法正确的是______.
A.样本中支出在![]() 元的频率为
元的频率为![]()
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2000名学生,则定有600人支出在![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 是函数
是函数![]() 的导函数,则
的导函数,则![]() 的图象大致是( )
的图象大致是( )
A. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/8f50d3dfba9b485fac00e42a95909498.png] B. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/74ae44978a70424c961e850ed79072da.png]
C. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/2f113f7ec5294ba0bbd1f66b13f3e152.png] D. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/dbaa9025ccdb497380b769e5396c4c19.png]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga( ![]() ﹣mx)在R上为奇函数,a>1,m>0. (Ⅰ)求实数m的值;
﹣mx)在R上为奇函数,a>1,m>0. (Ⅰ)求实数m的值;
(Ⅱ)指出函数f(x)的单调性.(不需要证明)
(Ⅲ)设对任意x∈R,都有f( ![]() cosx+2t+5)+f(
cosx+2t+5)+f( ![]() sinx﹣t2)≤0;是否存在a的值,使g(t)=a
sinx﹣t2)≤0;是否存在a的值,使g(t)=a ![]() ﹣2t+1最小值为﹣
﹣2t+1最小值为﹣ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com