
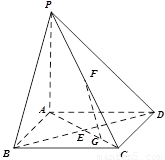
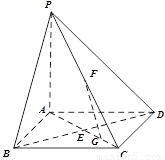
如图,在底面是正方形的四棱锥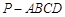 中,
中,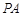
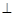 面
面 ,
,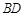 交
交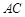 于点
于点 ,
,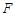 是
是 中点,
中点,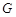 为
为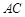 上一动点.
上一动点.
(1)求证: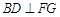 ;
;
(1)确定点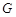 在线段
在线段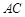 上的位置,使
上的位置,使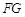 //平面
//平面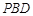 ,并说明理由.
,并说明理由.
(3)如果PA=AB=2,求三棱锥B-CDF的体积
⑴详见解析;⑵当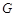 为
为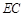 中点时,
中点时,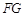 //平面
//平面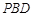 ;(3)三棱锥B-CDF的体积为
;(3)三棱锥B-CDF的体积为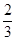 .
.
【解析】
试题分析:⑴证空间两直线垂直的常用方法是通过线面垂直来证明,本题中,由于直线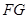 在平面
在平面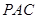 内,所以考虑证明
内,所以考虑证明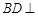 平面
平面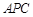 .⑵注意平面
.⑵注意平面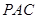 与平面
与平面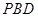 相交于
相交于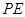 ,而直线
,而直线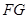 在平面
在平面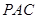 内,故只需
内,故只需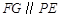 即可,而这又只需
即可,而这又只需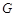 为
为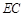 中点即可.(3)求三棱锥B-CDF的体积中转化为求三棱锥F-BCD的体积,这样底面面积与高都很易求得.
中点即可.(3)求三棱锥B-CDF的体积中转化为求三棱锥F-BCD的体积,这样底面面积与高都很易求得.
试题解析:⑴∵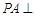 面
面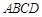 ,四边形
,四边形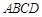 是正方形,
是正方形,
其对角线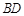 、
、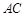 交于点
交于点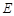 ,
,
∴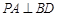 ,
,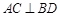 .2分
.2分
∴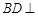 平面
平面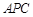 , 3分
, 3分
∵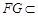 平面
平面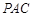 ,
,
∴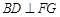 4分
4分
⑵当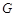 为
为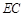 中点,即
中点,即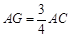 时,
时,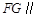 /平面
/平面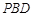 , 5分
, 5分
理由如下:
连结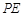 ,由
,由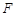 为
为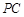 中点,
中点,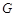 为
为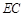 中点,知
中点,知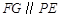 6分
6分
而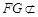 平面
平面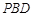 ,
,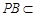 平面
平面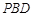 ,
,
故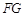 //平面
//平面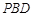 .
8分
.
8分
(3)三棱锥B-CDF的体积为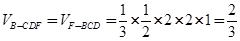 .12分
.12分
考点:1、空间直线与平面的关系;2、三棱锥的体积.


科目:高中数学 来源: 题型:
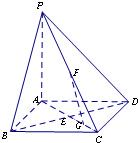 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:
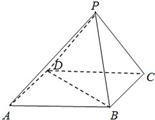 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.| 2π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:
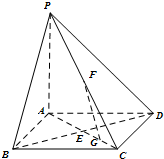 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com