
【题目】在平面直角坐标系![]() 中取两个定点
中取两个定点![]() ,
,![]() ,再取两个动点
,再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(1)求直线![]() 与
与![]() 的交点
的交点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴且与轨迹
轴且与轨迹![]() 交于另一点
交于另一点![]() ,
,![]() 为轨迹
为轨迹![]() 的右焦点,若
的右焦点,若![]() ,求证:
,求证:![]()
 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,直线
,直线![]() 与曲线y=f(x)和y=g(x)分别交于M,N两点,设曲线y=f(x)在点M处的切线为
与曲线y=f(x)和y=g(x)分别交于M,N两点,设曲线y=f(x)在点M处的切线为![]() ,在点N处的切线为
,在点N处的切线为![]()
(1)当b=1时,若![]() ,求a的值
,求a的值
(2)若![]() ,求实数a的取值范围
,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,且当n2时,![]()
(1)若=1,证明数列{a2n1}是等差数列;
(2)若=2.①设![]() ,求数列{bn}的通项公式;②设
,求数列{bn}的通项公式;②设![]() ,证明:对于任意的p,m N *,当p m,都有
,证明:对于任意的p,m N *,当p m,都有![]() Cm.
Cm.
查看答案和解析>>
科目:高中数学 来源: 题型:
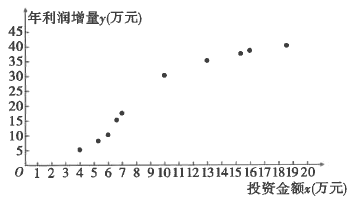
【题目】某果园种植“糖心苹果”已有十余年,为了提高利润,该果园每年投入一定的资金,对种植采摘包装宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额![]() (单位:万元)与年利润增量
(单位:万元)与年利润增量![]() (单位:万元)的散点图:
(单位:万元)的散点图:
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了![]() 关于
关于![]() 的两个回归模型;
的两个回归模型;
模型①:由最小二乘公式可求得![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() ;
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:![]() 的附近,对投资金额
的附近,对投资金额![]() 做交换,令
做交换,令![]() ,则
,则![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)分别利用这两个回归模型,预测投资金额为20万元时的年利润增量(结果保留两位小数);
(3)根据下列表格中的数据,比较两种模型的相关指数![]() ,并说明谁的预测值精度更高更可靠.
,并说明谁的预测值精度更高更可靠.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:样本![]() 的最小乘估计公式为
的最小乘估计公式为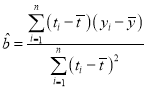 ,
,![]() ;
;
相关指数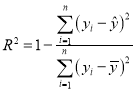 .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某果园种植“糖心苹果”已有十余年,根据其种植规模与以往的种植经验,产自该果园的单个“糖心苹果”的果径(最大横切面直径,单位:![]() )在正常环境下服从正态分布
)在正常环境下服从正态分布![]() .
.
(1)一顾客购买了20个该果园的“糖心苹果”,求会买到果径小于56![]() 的概率;
的概率;
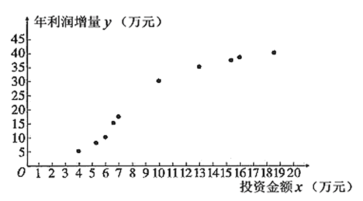
(2)为了提高利润,该果园每年投入一定的资金,对种植、采摘、包装、宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额![]() (单位:万元)与年利润增量
(单位:万元)与年利润增量![]() (单位:万元)的散点图:
(单位:万元)的散点图:
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了![]() 关于
关于![]() 的两个回归模型;
的两个回归模型;
模型①:由最小二乘公式可求得![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() ;
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:![]() 的附近,对投资金额
的附近,对投资金额![]() 做交换,令
做交换,令![]() ,则
,则![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测投资金额为20万元时的年利润增量(结果保留两位小数).
,并选择拟合精度更高、更可靠的模型,预测投资金额为20万元时的年利润增量(结果保留两位小数).
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:若随机变量![]() ,则
,则![]() ,
,![]() ;样本
;样本![]() 的最小乘估计公式为
的最小乘估计公式为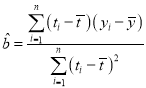 ,
,![]() ;
;
相关指数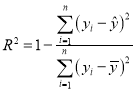 .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形且侧棱垂直与底面的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中,
的组合体中,![]() .
.
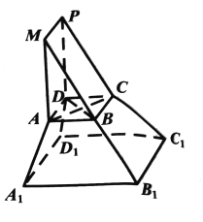
(1)证明:直线![]() 平面
平面![]() ;
;
(2)已知![]() ,且三棱锥A-A1B1D1的体积
,且三棱锥A-A1B1D1的体积![]() ,求该组合体的体积.
,求该组合体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),A(﹣a,0),B(0,﹣b),P为C上位于第一象限的动点,PA交y轴于点E,PB交x轴于点F.
1(a>b>0),A(﹣a,0),B(0,﹣b),P为C上位于第一象限的动点,PA交y轴于点E,PB交x轴于点F.
(1)探究四边形AEFB的面积是否为定值,说明理由;
(2)当△PEF的面积达到最大值时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com