
(满分12分)已知数列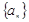 的前n项和
的前n项和 满足
满足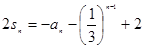 (n为正整数).
(n为正整数).
(1)令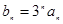 ,求证数列
,求证数列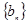 是等差数列,并求数列
是等差数列,并求数列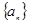 的通项公式;
的通项公式;
(2)令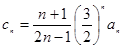 ,
,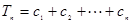 ,试比较
,试比较 与
与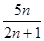 的大小,并予证明.
的大小,并予证明.
(I) ;
;
(II)当
 ,当
,当 时
,
时
,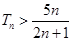 .证明见解析.
.证明见解析.
【解析】本试题主要是考查了数列的通项公式的求解和错位相减法求和的综合运用。
(1)借助于已知中的通项公式和前n项和的关系式,得到数列an的通项公式,然后利用 得到证明。
得到证明。
(2)根据上一问中的结论 ,然后结合错位相减法的数学思想,分析等比数列的公比,两边同乘以公比,再作差得到结论。
,然后结合错位相减法的数学思想,分析等比数列的公比,两边同乘以公比,再作差得到结论。
解:(I)令n=1,可得
当 时
时

 .
.
.
数列 是首项为1,公差为2的等差数列.
是首项为1,公差为2的等差数列.
 ..........................................4'
..........................................4'
(II)由(I)得 ,所以
,所以


由①-②得
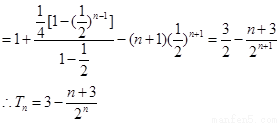 ........................8
........................8

于是确定 的大小关系等价于比较
的大小关系等价于比较 的大小
的大小
由
可猜想当 证明如下:
证明如下:
证法1:(1)当n=3时,由上验算显示成立。
(2)假设 时
时

所以当 时猜想也成立
时猜想也成立
综合(1)(2)可知 ,对一切 的正整数,都有
的正整数,都有 ...............12'
...............12'
证法2:当 时
时

综上所述,当
 ,当
,当 时
时


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源:2014届重庆市高二上学期期末考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)
已知数列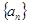 是递增数列,且满足
是递增数列,且满足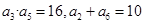 。
。
(1)若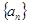 是等差数列,求数列
是等差数列,求数列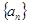 的通项公式;
的通项公式;
(2)对于(1)中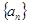 ,令
,令 ,求数列
,求数列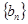 的前
的前 项和
项和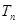 。
。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年新疆乌鲁木齐地区高三第一次诊断性测验文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知数列{an}、{bn}分别是首项均为2的各项均为正数的等比数列和等差数列,且

(I) 求数列{an}、{bn}的通项公式;
(II )求使 <0.001成立的最小的n值.
<0.001成立的最小的n值.
查看答案和解析>>
科目:高中数学 来源:2014届四川省高一下学期期中理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列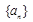 满足
满足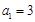 ,
,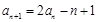 (
(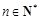 ).
).
(Ⅰ) 证明数列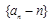 是等比数列,并求出数列
是等比数列,并求出数列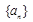 的通项公式;
的通项公式;
(Ⅱ)设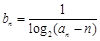 ,数列
,数列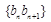 的前n项和为
的前n项和为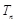 ,若对于任意
,若对于任意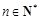 ,都满足
,都满足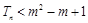 成立,求实数m的取值范围.
成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建厦门双十中学高三考前热身训练文数试卷 题型:解答题
(本题满分12分)
已知数列 的前
的前 项和为
项和为 ,且
,且 (
( ).
).
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)若数列 满足
满足 ,且
,且 ,求数列
,求数列 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省高三第三次考试理科数学卷 题型:解答题
(本题满分12分)已知数列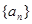 的前n项和为
的前n项和为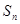 ,对一切正整数n,点
,对一切正整数n,点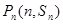 都在函数
都在函数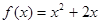 的图像上,且在点
的图像上,且在点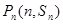 处的切线的斜率为
处的切线的斜率为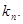
(I)求数列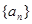 的通项公式;
的通项公式;
(II)若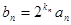 ,求数列
,求数列 的前n项和
的前n项和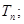
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com