解:(Ⅰ)由e2= =
=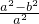 =1-
=1- =
= ,得a=
,得a= b
b
由点A(0,a),B(-b,0)知直线AB的方程为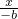 +
+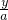 =1,即lAB:4x-3y+4b=0
=1,即lAB:4x-3y+4b=0
又原点O到直线AB的距离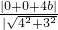 =
= b=
b= ,∴b=3,
,∴b=3,
∴b2=9,a2=16
从而椭圆M的方程为: +
+ =1.
=1.
(Ⅱ)易知P(3,0),设C(x1,y1),(x2,y2),将x=my+n代入 +
+ =1化简整理得
=1化简整理得
(16m2+9)y2+32mny+16n2-144=0
则y1+y2=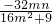 ,y1y2=
,y1y2=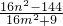 .
.
而 •
• =0?(x1-3,y1)•(x2-3,y2)=0即(x1-3)•(x2-3)+y1y2=0
=0?(x1-3,y1)•(x2-3,y2)=0即(x1-3)•(x2-3)+y1y2=0
又x1=my1+nn,x2=my2+nn
∴(my1+n-3)•(my2+n-3)+y1y2=0,
整理得(m2+1)y1y2+m(n-3)(y1+y2)+(n-3)2=0
即(m2+1)×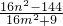 +m(n-3)×
+m(n-3)×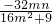 +(n-3)2=0
+(n-3)2=0
易知n≠3,∴16(m2+1)(n+3)-32m2n+(16m2+9)(n-3)=0
展开得25n+21=0?n=-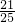
∴直线l的横截距n为定值
分析:(Ⅰ)由e
2=

=
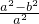
=1-

=

,得a=

b,由点A(0,a),B(-b,0)知直线AB的方程为
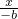
+
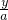
=1,再由点O到直线AB的距离
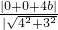
=

b=

,知b=3,由此能够得到椭圆M的方程.
(Ⅱ)P(3,0),设C(x
1,y
1),(x
2,y
2),将x=my+n代入

+

=1,得(16m
2+9)y
2+32mny+16n
2-144=0,则y
1+y
2=
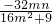
,y
1y
2=
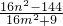
.由

•

=0,知(x
1-3)•(x
2-3)+y
1y
2=0,由x
1=my
1+nn,x
2=my
2+nn,知(my
1+n-3)•(my
2+n-3)+y
1y
2=0,由此能够证明直线l的横截距n为定值.
点评:本题考查椭圆方程的求法和直线l的横截距n为定值的证明,解题时要注意椭圆性质的灵活运用和合理地进行等价转化.

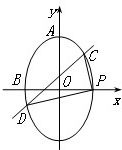 设椭圆M:
设椭圆M: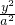 +
+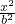 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,点A(0,a),B(-b,0),原点O到直线AB的距离为
,点A(0,a),B(-b,0),原点O到直线AB的距离为 ,P是椭圆的右顶点,直线l:x=my-n与椭圆M相交于C,D两点,且
,P是椭圆的右顶点,直线l:x=my-n与椭圆M相交于C,D两点,且 ⊥
⊥ .
. =
=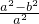 =1-
=1- =
= ,得a=
,得a= b
b 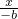 +
+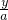 =1,即lAB:4x-3y+4b=0
=1,即lAB:4x-3y+4b=0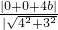 =
= b=
b= ,∴b=3,
,∴b=3, +
+ =1.
=1. +
+ =1化简整理得
=1化简整理得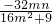 ,y1y2=
,y1y2=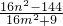 .
. •
• =0?(x1-3,y1)•(x2-3,y2)=0即(x1-3)•(x2-3)+y1y2=0
=0?(x1-3,y1)•(x2-3,y2)=0即(x1-3)•(x2-3)+y1y2=0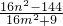 +m(n-3)×
+m(n-3)×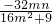 +(n-3)2=0
+(n-3)2=0 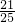
 =
=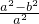 =1-
=1- =
= ,得a=
,得a= b,由点A(0,a),B(-b,0)知直线AB的方程为
b,由点A(0,a),B(-b,0)知直线AB的方程为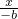 +
+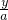 =1,再由点O到直线AB的距离
=1,再由点O到直线AB的距离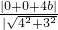 =
= b=
b= ,知b=3,由此能够得到椭圆M的方程.
,知b=3,由此能够得到椭圆M的方程. +
+ =1,得(16m2+9)y2+32mny+16n2-144=0,则y1+y2=
=1,得(16m2+9)y2+32mny+16n2-144=0,则y1+y2=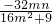 ,y1y2=
,y1y2=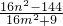 .由
.由 •
• =0,知(x1-3)•(x2-3)+y1y2=0,由x1=my1+nn,x2=my2+nn,知(my1+n-3)•(my2+n-3)+y1y2=0,由此能够证明直线l的横截距n为定值.
=0,知(x1-3)•(x2-3)+y1y2=0,由x1=my1+nn,x2=my2+nn,知(my1+n-3)•(my2+n-3)+y1y2=0,由此能够证明直线l的横截距n为定值.

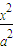 +
+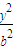 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为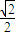 ,点A(a,0),B(0,-b),原点O到直线AB的距离为
,点A(a,0),B(0,-b),原点O到直线AB的距离为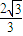 .
.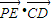 =0,|
=0,|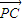 |=|
|=|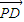 |,试求△PCD面积S的最大值.
|,试求△PCD面积S的最大值. +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,点A(0,a),B(-b,0),原点O到直线AB的距离为
,点A(0,a),B(-b,0),原点O到直线AB的距离为 ,P是椭圆的右顶点,直线l:x=my-n与椭圆M相交于C,D两点,且
,P是椭圆的右顶点,直线l:x=my-n与椭圆M相交于C,D两点,且 ⊥
⊥ .
.