
命题p:∃x∈R,使得x2+(a﹣1)x+1<0,命题q:∀x∈R,ax2+x+1>0恒成立.若p或q为真命题,p且q为假命题,求实数a的取值范围.
科目:高中数学 来源: 题型:
下列命题中正确的是 ( )
A.若p∨q为真命题,则p∧q为真命题
B.“x=5”是“x2-4x-5=0”的充分不必要条件
C.命题“若x<-1,则x2-2x-3>0”的否定为:“若x≥-1,则x2-2x-3≤0”
D.已知命题p:∃x∈R,x2+x-1<0,则綈p:∃x∈R,x2+x-1≥0
查看答案和解析>>
科目:高中数学 来源:2014届湖南师大附中高三第二次月考理科数学试卷(解析版) 题型:选择题
已知命题p:∃x∈R,x2-3x+3≤0,则下列说法正确的是 ( )
A.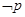 :∃x∈R,
:∃x∈R,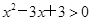 ,且
,且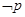 为真命题
为真命题
B.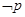 :∃x∈R,
:∃x∈R,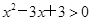 ,且
,且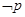 为假命题
为假命题
C.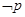 :∀x∈R,
:∀x∈R,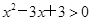 ,且
,且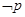 为真命题
为真命题
D.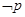 :∀x∈R,
:∀x∈R,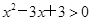 ,且
,且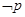 为假命题
为假命题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省长春市高三上学期期初考试理科数学试卷(解析版) 题型:选择题
下列说法错误的个数为( )
①命题“若 ,则一元二次方程
,则一元二次方程 有实根”的逆否命题是真命题
有实根”的逆否命题是真命题
②“x2-3x+2=0”是“x=2”的必要不充分条件
③命题“若xy=0,则x,y中至少有一个为零”的否定是:“若xy≠0,则x,y都不为零”
④命题p:∃x∈R,使得x2+x+1 0;则
0;则 p:∀x∈R,均有x2+x+1
p:∀x∈R,均有x2+x+1 0
0
⑤若命题 p为真,
p为真, 为假,则命题
为假,则命题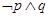 为真,
为真, 为假
为假
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省高三上学期期末考试数学理卷 题型:选择题
下列说法错误的是 ( )
A.命题:“已知f(x)是R上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题
 B.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+1≥0”
B.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+1≥0”
C.若p且q为假命题,则p、q均为假命题
D.“x>1”是“|x|>1”的充分不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com