
【题目】必修四第一章我们借助圆的对称性学习了诱导公式,如![]() 在直观上讲单位圆中,当两个角的终边关于
在直观上讲单位圆中,当两个角的终边关于![]() 轴对称时,这两个角的正弦值相等;再如
轴对称时,这两个角的正弦值相等;再如![]() 在单位圆中,当两个角的终边关于原点中心对称时,这两个角的正弦值互为相反数.观察这些诱导公式,可以发现它们都是特殊角与任意角
在单位圆中,当两个角的终边关于原点中心对称时,这两个角的正弦值互为相反数.观察这些诱导公式,可以发现它们都是特殊角与任意角![]() 的三角函数的恒等关系.我们如果将特殊角换为任意角
的三角函数的恒等关系.我们如果将特殊角换为任意角![]() ,那么任意角
,那么任意角![]() 与
与![]() 的和(或差)的三角函数与
的和(或差)的三角函数与![]() ,
,![]() 的三角函数会有什么关系呢?如果已知
的三角函数会有什么关系呢?如果已知![]() ,
,![]() 的正弦余弦,能由此推出
的正弦余弦,能由此推出![]() 的正弦余弦吗?下面是某高一学生在老师的指导下自行探究
的正弦余弦吗?下面是某高一学生在老师的指导下自行探究![]() 与角
与角![]()
![]() 的正弦余弦之间的关系的部分过程,请你顺着这位同学的思路以及老师的提示将探究过程完善,并完成后面的题目.探究过程如下:
的正弦余弦之间的关系的部分过程,请你顺着这位同学的思路以及老师的提示将探究过程完善,并完成后面的题目.探究过程如下:
不妨令![]() 如图,设单位圆与
如图,设单位圆与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() 以
以![]() 轴的非负半轴为始边作角
轴的非负半轴为始边作角![]() 它们的终边分别与单位圆相交于点
它们的终边分别与单位圆相交于点![]() 连接
连接![]() 若把扇形
若把扇形![]() 绕着点
绕着点![]() 旋转
旋转![]() 角,则点
角,则点![]() 分别与点
分别与点![]() 重合. ……(未完待续)
重合. ……(未完待续)
(提示一:任意一个圆绕着其圆心旋转任意角后都与原来的圆重合,这一性质叫做圆的旋转对称性)(提示二:平面上任意两点![]() 间的距离公式
间的距离公式![]() )
)
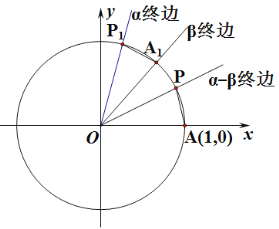
(1)完善上述探究过程;
(2)利用(1)中的结论解决问题:已知![]()
![]() 是第三象限角,求
是第三象限角,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左.右焦点为
的左.右焦点为![]() ,离心率为
,离心率为![]() .直线
.直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() 是直线
是直线![]() 与椭圆
与椭圆![]() 的一个公共点,
的一个公共点,![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,设
的对称点,设![]() .
.
(1)证明:![]() ;
;
(2)若![]() ,
,![]() 的周长为
的周长为![]() ;写出椭圆
;写出椭圆![]() 的方程;
的方程;
(3)确定![]() 的值,使得
的值,使得![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·衡水二模)某商场在元旦举行购物抽奖促销活动,规定顾客从装有编号0,1,2,3,4的五个相同小球的抽奖箱中一次任意摸出两个小球,若取出的两个小球的编号之和等于7则中一等奖,等于6或5则中二等奖,等于4则中三等奖,其余结果为不中奖.
(1)求中二等奖的概率.
(2)求不中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,三个内角
中,三个内角![]() ,
,![]() ,
,![]() 所对的边分别是
所对的边分别是![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() ;
;
(2)在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个补充在下面问题中,并解答
这三个条件中任选一个补充在下面问题中,并解答
若![]() ,
,![]() ,________,求
,________,求![]() 的周长.
的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年某市有2万多文科考生参加高考,除去成绩为![]() 分(含
分(含![]() 分)以上的3人与成绩为
分)以上的3人与成绩为![]() 分(不含
分(不含![]() 分)以下的3836人,还有约1.9万文科考生的成绩集中在
分)以下的3836人,还有约1.9万文科考生的成绩集中在![]() 内,其成绩的频率分布如下表所示:
内,其成绩的频率分布如下表所示:
分数段 |
|
|
|
|
频率 | 0.108 | 0.133 | 0.161 | 0.183 |
分数段 |
|
|
|
|
频率 | 0.193 | 0.154 | 0.061 | 0.007 |
(Ⅰ)试估计该次高考成绩在![]() 内文科考生的平均分(精确到
内文科考生的平均分(精确到![]() );
);
(Ⅱ)一考生填报志愿后,得知另外有4名同分数考生也填报了该志愿.若该志愿计划录取3人,并在同分数考生中随机录取,求该考生不被该志愿录取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量, ![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
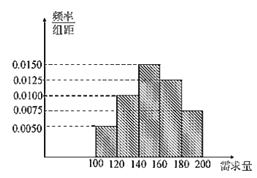
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数;
的平均数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于4000元的概率.
不少于4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下四种变换方式:
![]() 向左平移
向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ;
;
![]() 向左平移
向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ;
;
![]() 把各点的横坐标缩短到原来的
把各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ,再向左平移
,再向左平移![]() 个单位长度;
个单位长度;
![]() 把各点的横坐标缩短到原来的
把各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ,再向左平移
,再向左平移![]() 个单位长度;
个单位长度;
其中能将函数![]() 的图象变为函数
的图象变为函数![]() 的图象的是
的图象的是![]()
![]()
A. ![]() 和
和![]() B.
B. ![]() 和
和![]() C.
C. ![]() 和
和![]() D.
D. ![]() 和
和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,坐标原点为
,坐标原点为![]() .椭圆
.椭圆![]() 的动弦
的动弦![]() 过右焦点
过右焦点![]() 且不垂直于坐标轴,
且不垂直于坐标轴, ![]() 的中点为
的中点为![]() ,过
,过![]() 且垂直于线段
且垂直于线段![]() 的直线交射线
的直线交射线![]() 于点
于点![]()
(I)证明:点![]() 在直线
在直线![]() 上;
上;
(Ⅱ)当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com