
【题目】已知函数![]() ,若函数
,若函数![]() 恰有7个不同零点,则实数a的取值范围是( )
恰有7个不同零点,则实数a的取值范围是( )
A.(0,1)B.[-1,1]C.(-1,1)D.(-1,0)∪(0,1)
【答案】D
【解析】
利用十字相乘法法进行因式分解,然后利用换元法![]() ,作出
,作出![]() 的图象,利用数形结合判断根的个数即可,
的图象,利用数形结合判断根的个数即可,
由![]()
得:![]()
则![]() 或
或![]() ,
,
作出![]() 的图象如图,
的图象如图,
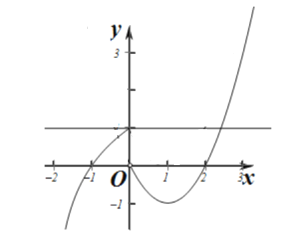
则若![]() ,则
,则![]() 或
或![]() ,
,
设![]() ,由
,由![]() 得
得![]() ,
,
此时![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,有两个根,当
,有两个根,当![]() 时,
时,![]() ,有1个根,
,有1个根,
则必须有![]() ,
,![]() 有4个根,
有4个根,
设![]() ,由
,由![]() 得
得![]() ,
,
若![]() ,由
,由![]() 得
得![]() ,或
,或![]() ,
,![]() 有2个根,
有2个根,![]() 有1个根,
有1个根,
此时有3个根,不满足条件.
若![]() ,由
,由![]() 得
得![]() ,
,![]() 有1个根,不满足条件.
有1个根,不满足条件.
若![]() ,由
,由![]() 得
得![]() ,或
,或![]()
当![]() 时,
时,![]() ,有3个根,
,有3个根,
当![]() 时,
时,![]() ,有1个根,
,有1个根,
此时有![]() 个根,满足条件.
个根,满足条件.
若![]() ,由
,由![]() 得
得![]() 或
或![]() ,
,
![]() 有1个根,
有1个根,![]() 有2个根,
有2个根,
此时有3个根,不满足条件.
若![]() ,由
,由![]() 得
得![]() ,或
,或![]() 或
或![]()
当![]() 时,
时,![]() 有1个根,
有1个根,
当![]() 时,
时,![]() 有2个根,
有2个根,
当![]() 时,
时,![]() 有1个根,
有1个根,
此时有![]() 个根,满足条件.
个根,满足条件.
若![]() ,由
,由![]() 得
得![]() ,
,
![]() 有1个根,不满足题意.
有1个根,不满足题意.
综上,a的取值范围是![]() .
.
故选:D.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(x+1)+x2+1,g(x)=﹣x2﹣2mx+4.
(1)当a>0时,求曲线y=f(x)的切线斜率的取值范围;
(2)当a=﹣4时,若存在x1∈[0,1],x2∈[1,2],满足f(x1)≥g(x2),求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (c为常数),且f(1)=0.
(c为常数),且f(1)=0.
(1)求c的值;
(2)证明函数f(x)在[0,2]上是单调递增函数;
(3)已知函数g(x)=f(ex),判断函数g(x)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
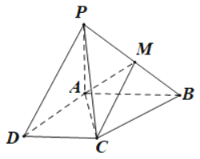
【题目】如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB//DC,![]() ,PA
,PA![]() 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=![]() AB=1,M是PB的中点.
AB=1,M是PB的中点.
(1)证明:面PAD![]() 面PCD;
面PCD;
(2)求AC与PB所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资额成正比,设比例系数为![]() ,其关系如图1;B产品的利润与投资额的算术平方根成正比,设比例系数为
,其关系如图1;B产品的利润与投资额的算术平方根成正比,设比例系数为![]() ,其关系如图2.(注:利润与投资额单位是万元)
,其关系如图2.(注:利润与投资额单位是万元)
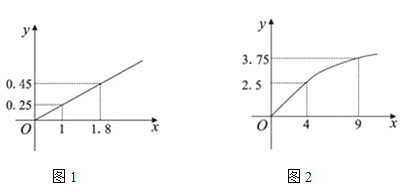
(1)分别将A,B两种产品的利润表示为投资额的函数,并求出![]()
![]() 的值,写出它们的函数关系式;
的值,写出它们的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资额,才能使企业获得最大利润,其最大利润为多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com