Question

（18）请您设计一个帐篷。它下部的形状是高为1m的正六棱柱，上部的形状是侧棱长为3m的正六棱锥（如下图所示）。试问当帐篷的顶点O到底面中心O₁的距离为多少时，帐篷的体积最大？

Answer 1

本小题主要考查利用导数研究函数的最大值和最小值的基础知识，以及运用数学知识解决实际问题的能力.

解：设OO₁为xm，则1＜x＜4.

由题设可得正六棱锥底面边长为（单位：m）

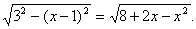
于是底面正六边形的面积为（单位：m²）

 

 

 

 

 

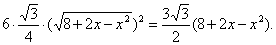
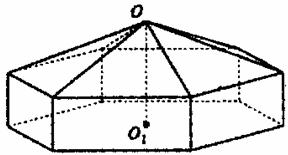
帐篷的体积为（单位：m³）

V（x）=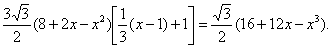

求导数，得V′（x）=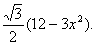

令V′（x）=0，解得x=-2（不合题意，舍去），x=2.

当1＜x＜2时，V′（x）＞0，V（x）为增函数;

当2＜x＜4时，V′（x）＜0，V（x）为减函数.

所以当x=2时，V（x）最大.

答：当OO₁为2m时，帐篷的体积最大.