
【题目】如图,菱形![]() 的边长为12,
的边长为12,![]() ,
,![]() 与
与![]() 交于
交于![]() 点,将菱形
点,将菱形![]() 沿对角线
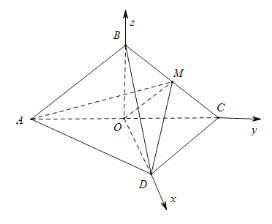
沿对角线![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() .
.
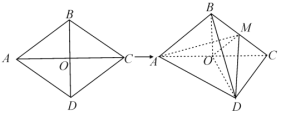
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)根据题意,由菱形的性质可知![]() 和
和![]() ,由直角三角形斜边上的中线的性质得出
,由直角三角形斜边上的中线的性质得出![]() ,利用勾股定理的逆定理得出
,利用勾股定理的逆定理得出![]() ,根据线面垂直的判定定理即可证出
,根据线面垂直的判定定理即可证出![]() 平面
平面![]() ,最后由线面垂直的性质得出
,最后由线面垂直的性质得出![]() ;
;
(2)根据菱形对角线的性质得出![]() ,
,![]() ,线面垂直的判定定理得出
,线面垂直的判定定理得出![]() 平面
平面![]() ,建立空间直角坐标系,分别求出平面
,建立空间直角坐标系,分别求出平面![]() 和平面
和平面![]() 的法向量,利用空间向量法求二面角的公式,即可求出二面角
的法向量,利用空间向量法求二面角的公式,即可求出二面角![]() 的余弦值.
的余弦值.
证明:(1)∵四边形![]() 是菱形,且边长为12,
是菱形,且边长为12,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,又
,又![]() 是
是![]() 中点,
中点,
∴![]() ,
,
又![]() ,
,
则![]() ,∴
,∴![]() ,
,
又![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() .
.
解:(2)由题意,![]() ,
,![]() ,
,
又由(1)知![]() ,
,
且![]() 平面
平面![]() ,
,![]() ,则
,则![]() 平面
平面![]() ,
,
故以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 方向为
方向为![]() 、
、![]() 、
、![]() 轴正向建立空间直角坐标系,
轴正向建立空间直角坐标系,
由于![]() ,则
,则![]() ,
,
易知![]() ,
,![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则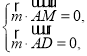 ,
,
即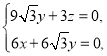 令
令![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
由于已证![]() 平面
平面![]() ,故平面
,故平面![]() 的法向量为
的法向量为![]() ,
,
所以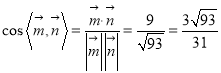 ,
,
由图知二面角![]() 为锐二面角,故其余弦值为
为锐二面角,故其余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】高二某班共有45人,学号依次为1、2、3、…、45,现按学号用系统抽样的办法抽取一个容量为5的样本,已知学号为6、24、33的同学在样本中,那么样本中还有两个同学的学号应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】互联网正在改变着人们的生活方式,在日常消费中手机支付正逐渐取代现金支付成为人们首选的支付方式. 某学生在暑期社会活动中针对人们生活中的支付方式进行了调查研究. 采用调查问卷的方式对100名18岁以上的成年人进行了研究,发现共有60人以手机支付作为自己的首选支付方式,在这60人中,45岁以下的占![]() ,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
(1)从以现金作为首选支付方式的40人中,任意选取3人,求这3人至少有1人的年龄低于45岁的概率;
(2)某商家为了鼓励人们使用手机支付,做出以下促销活动:凡是用手机支付的消费者,商品一律打八折. 已知某商品原价50元,以上述调查的支付方式的频率作为消费者购买该商品的支付方式的概率,设销售每件商品的消费者的支付方式都是相互独立的,求销售10件该商品的销售额的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
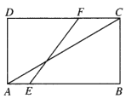
【题目】矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的动点,将矩形
上的动点,将矩形![]() 沿
沿![]() 所在的直线进行随意翻折,在翻折过程中直线
所在的直线进行随意翻折,在翻折过程中直线![]() 与直线
与直线![]() 所成角的范围(包含初始状态)为( )
所成角的范围(包含初始状态)为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,武汉发生“新型冠状病毒”肺炎疫情,国家卫健委紧急部署,从多省调派医务工作者前去支援,正值农历春节举家团圆之际,他们成为“最美逆行者”.武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者疑似的新冠肺炎患者无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户不漏一人.若在排查期间,某小区有5人被确认为“确诊患者的密切接触者”,现医护人员要对这5人随机进行逐一“核糖核酸”检测,只要出现一例阳性,则将该小区确定为“感染高危小区”.假设每人被确诊的概率均为![]() 且相互独立,若当
且相互独立,若当![]() 时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则
时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则![]() ____.
____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估![]() 设备生产某种零件的性能,从该设备生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
设备生产某种零件的性能,从该设备生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 78 | 79 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 93 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的频率):
表示相应事件的频率):
①![]() ;②
;②![]() ;③
;③![]() ,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断
,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断![]() 设备的性能等级.
设备的性能等级.
(2)将直径小于等于![]() 的零件或直径大于等于
的零件或直径大于等于![]() 的零件认定为是“次品”,将直径小于等于
的零件认定为是“次品”,将直径小于等于![]() 的零件或直径大于等于
的零件或直径大于等于![]() 的零件认定为是“突变品”,从样本的“次品”中随意抽取2件零件,求“突变品”个数
的零件认定为是“突变品”,从样本的“次品”中随意抽取2件零件,求“突变品”个数![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 相切于点
相切于点![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)求抛物线![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)设![]() 是
是![]() 轴上两个不同的动点,且满足
轴上两个不同的动点,且满足![]() ,直线
,直线![]() 、
、![]() 与抛物线
与抛物线![]() 的另一个交点分别为
的另一个交点分别为![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.如果相交,求出的交点的坐标.
的位置关系,并说明理由.如果相交,求出的交点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 与函数
与函数![]() 满足:①
满足:①![]() 的任意两项均不相等,且
的任意两项均不相等,且![]() 的定义域为
的定义域为![]() ;②数列
;②数列![]() 的前
的前![]() 的项的和
的项的和![]() 对任意的
对任意的![]() 都成立,则称
都成立,则称![]() 与
与![]() 具有“共生关系”.
具有“共生关系”.
(1)若![]() ,试写出一个与数列
,试写出一个与数列![]() 具有“共生关系”的函数
具有“共生关系”的函数![]() 的解析式;
的解析式;
(2)若![]() 与数列
与数列![]() 具有“共生关系”,求实数对
具有“共生关系”,求实数对![]() 所构成的集合,并写出
所构成的集合,并写出![]() 关于
关于![]() ,
,![]() ,
,![]() 的表达式;
的表达式;
(3)若![]() ,求证:“存在每项都是正数的无穷等差数列
,求证:“存在每项都是正数的无穷等差数列![]() ,使得
,使得![]() 与
与![]() 具有‘共生关系’”的充要条件是“点
具有‘共生关系’”的充要条件是“点![]() 在射线
在射线![]() 上”.
上”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com