
【题目】在平面直角坐标系中,以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,点![]() ,(
,(![]() )在曲线C:
)在曲线C:![]() 上,直线l过点
上,直线l过点![]() 且与
且与![]() 垂直,垂足为P.
垂直,垂足为P.
(Ⅰ)当![]() 时,求在直角坐标系下点P坐标和l的方程;
时,求在直角坐标系下点P坐标和l的方程;
(Ⅱ)当M在C上运动且P在线段![]() 上时,求点P在极坐标系下的轨迹方程.
上时,求点P在极坐标系下的轨迹方程.
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某中学长期坚持贯彻以人为本,因材施教的教育理念,每年都会在校文化节期间举行“数学素养能力测试”和“语文素养能力测试”两项测试,以给学生课外兴趣学习及辅导提供参考依据.成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级(等级
五个等级(等级![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别对应5分,4分,3分,2分,1分).某班学生两科的考试成绩的数据统计如图所示,其中“语文素养能力测试”科目的成绩为
分别对应5分,4分,3分,2分,1分).某班学生两科的考试成绩的数据统计如图所示,其中“语文素养能力测试”科目的成绩为![]() 的考生有3人.
的考生有3人.
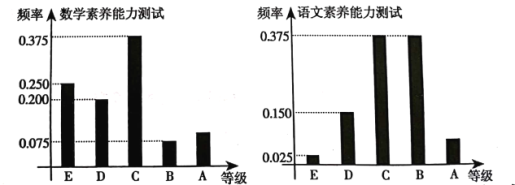
(1)求该班“数学素养能力测试”的科目平均分以及“数学素养能力测试”科目成绩为![]() 的人数;
的人数;
(2)若该班共有9人得分大于7分,其中有2人10分,3人9分,4人8分.从这9人中随机抽取三人,设三人的成绩之和为![]() ,求
,求![]() .
.
(3)从该班得分大于7分的9人中选3人即甲,乙,丙组队参加学校内的“数学限时解题挑战赛”.规则为:每队首先派一名队员参加挑战赛,在限定的时间,若该生解决问题,即团队挑战成功,结束挑战;若解决问题失败,则派另外一名队员上去挑战,直至派完队员为止.通过训练,已知甲,乙,丙通过挑战赛的概率分别是![]() ,
,![]() ,
,![]() ,问以怎样的先后顺序派出队员,可使得派出队员数目的均值达到最小?(只需写出结果)
,问以怎样的先后顺序派出队员,可使得派出队员数目的均值达到最小?(只需写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的棱长均为6,其内有
的棱长均为6,其内有![]() 个小球,球
个小球,球![]() 与三棱锥
与三棱锥![]() 的四个面都相切,球
的四个面都相切,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切,如此类推,…,球
都相切,如此类推,…,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切(
都相切(![]() ,且
,且![]() ),则球
),则球![]() 的体积等于__________,球
的体积等于__________,球![]() 的表面积等于__________.
的表面积等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (t为参数),以坐标原点为极点,
(t为参数),以坐标原点为极点,![]() 正半轴为极轴,建立极坐标系,曲线
正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 到直线
到直线![]() 距离的最小值,并求出此时
距离的最小值,并求出此时![]() 点坐标.
点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是各项均为正数的无穷数列,数列
是各项均为正数的无穷数列,数列![]() 满足
满足![]() (n
(n![]() ),其中常数k为正整数.
),其中常数k为正整数.
(1)设数列![]() 前n项的积
前n项的积![]() ,当k=2时,求数列
,当k=2时,求数列![]() 的通项公式;
的通项公式;
(2)若![]() 是首项为1,公差d为整数的等差数列,且
是首项为1,公差d为整数的等差数列,且![]() =4,求数列
=4,求数列![]() 的前2020项的和;
的前2020项的和;
(3)若![]() 是等比数列,且对任意的n
是等比数列,且对任意的n![]() ,
,![]() ,其中k≥2,试问:
,其中k≥2,试问:![]() 是等比数列吗?请证明你的结论.
是等比数列吗?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 和
和![]() 两点.
两点.
(1)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)若过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,记
两点,记![]() 与
与![]() 的面积分别为
的面积分别为![]() 与
与![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com