【题目】已知函数 
，若将f（x）的图象向左平移 
个单位后所得函数的图象关于原点对称，则φ=（ ）
A.
B.
C.
D.
【答案】B
【解析】解：∵函数 
， ∴sinφ=﹣sin（ω 
+φ），∴ω=4k+2，k∈Z．
将f（x）=sin（ωx+φ）的图象向左平移 
个单位后所得函数的解析式为y=sin（ωx+ 
+φ）的图象关于原点对称，
∴ +φ=lπ，l∈Z，∵φ∈（0， ）∴k=2，ω=10，此时，φ= 
，
故选：B．
【考点精析】通过灵活运用函数y=Asin（ωx+φ）的图象变换，掌握图象上所有点向左（右）平移
个单位长度，得到函数
的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的
倍（纵坐标不变），得到函数
的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的
倍（横坐标不变），得到函数
的图象即可以解答此题．
科目：高中数学 来源： 题型：
【题目】在△ABC中，设边a，b，c所对的角分别为A，B，C，且a＞c．已知△ABC的面积为 
， 
，b=3．
（Ⅰ）求a，c的值；
（Ⅱ）求sin（B﹣C）的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4-5：不等式选讲]
设函数f（x）=|x+ 
|+|x﹣2m|（m＞0）．
（Ⅰ）求证：f（x）≥8恒成立；
（Ⅱ）求使得不等式f（1）＞10成立的实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线C： 
﹣ 
=1（a＞0，b＞0）的左焦点为F，第二象限的点M在双曲线C的渐近线上，且|OM|=a，若直线MF的斜率为 
，则双曲线C的渐近线方程为（ ）
A.y=±x
B.y=±2x
C.y=±3x
D.y=±4x
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，设椭圆 
=1（a＞b＞0）的左、右焦点分别为F1 ， F2 ， 右顶点为A，上顶点为B，离心率为e．椭圆上一点C满足：C在x轴上方，且CF1⊥x轴．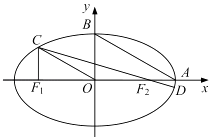
（1）若OC∥AB，求e的值；
（2）连结CF2并延长交椭圆于另一点D若 
≤e≤ 
，求 
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD都是边长为2的等边三角形，E是BC的中点． 
（1）求证：AE∥平面PCD；
（2）记平面PAB与平面PCD的交线为l，求二面角C﹣l﹣B的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】三棱锥P﹣ABC中，底面△ABC满足BA=BC， 
，P在面ABC的射影为AC的中点，且该三棱锥的体积为 
，当其外接球的表面积最小时，P到面ABC的距离为（ ）
A.2
B.3
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点P（x，y）是曲线C上任意一点，点（x，2y）在圆x2+y2=8上，定点M（2，1），平行于OM的直线l在y轴上的截距为m（m≠0），直线l与曲线C交于A、B两个不同点．
（1）求曲线C的方程；
（2）求证直线MA、MB与x轴始终围成一个等腰三角形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
