
【题目】已知平行四边形ABCD的三个顶点的坐标为A(﹣1,5),B(﹣2,﹣1),C(2,3).
(1)求平行四边形ABCD的顶点D的坐标;
(2)在△ACD中,求CD边上的高所在直线方程;
(3)求四边形ABCD的面积.
【答案】
(1)解:解法一:设D(x,y),
∵A(﹣1,5),B(﹣2,﹣1),C(2,3), ![]() ,
,
∴(﹣1,﹣6)=(2﹣x,3﹣y),
∴x=3,y=9,即D(3,9).
解法二:∵A(﹣1,5),B(﹣2,﹣1),C(2,3),
∴AC中点为 ![]() ,
,
该点也为BD中点,设D(x,y),
则可得D(3,9)
(2)解:∵A(﹣1,5),B(﹣2,﹣1),C(2,3),
∴CD边的斜率kCD= ![]() =6,
=6,
∴CD边上的高的斜率为 ![]() ,
,
∴CD边上的高所在的直线方程为y﹣5=﹣ ![]() (x+1),即x+6y﹣29=0
(x+1),即x+6y﹣29=0
(3)解:解法一:∵B(﹣2,﹣1),C(2,3).
∴直线BC: ![]() =
= ![]() ,即x﹣y+1=0,
,即x﹣y+1=0,
∴A到BC的距离为d= ![]() ,
,
又BC= ![]() =4
=4 ![]() ,
,
∴四边形ABCD的面积为 ![]() .
.
解法二:∵ ![]() ,
, ![]() ,
, ![]()
∴由余弦定理得 ![]()
∴ ![]()
∴四边形ABCD的面积为 ![]()
【解析】(1)可以利用平行四边形的一组对边平行,借助向量求得点D的坐标;也可以利用平行四边形的两条对角线互相平分,借助中点坐标公式求得点D的坐标;(2)利用两条互相垂直的直线的斜率积为-1,由直线CD的斜率求得其边上高的斜率,又过点A,进而求得CD边上的高所在的直线方程;(3)可以利用一边与其边上的高求得平行四边形的面积,也可以利用:一条对角线将三角形分为两个面积相等的三角形,来求平行四边形的面积.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知一个袋中装有大小相同的4个红球,3个白球,3个黄球.若任意取出2个球,则取出的2个球颜色相同的概率是;若有放回地任意取10次,每次取出一个球,每取到一个红球得2分,取到其它球不得分,则得分数X的方差为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(1,2),B(﹣3,﹣1),若圆x2+y2=r2(r>0)上恰有两点M,N,使得△MAB和△NAB的面积均为5,则r的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,B(0,2),C(1,0),斜率为
,B(0,2),C(1,0),斜率为 ![]() 的直线l过点A,且l和以C为圆心的圆相切.
的直线l过点A,且l和以C为圆心的圆相切.
(1)求圆C的方程;
(2)在圆C上是否存在点P,使得 ![]() ,若存在,求出所有的点P的坐标;若不存在说明理由;
,若存在,求出所有的点P的坐标;若不存在说明理由;
(3)若不过C的直线m与圆C交于M,N两点,且满足CM,MN,CN的斜率依次为等比数列,求直线m的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
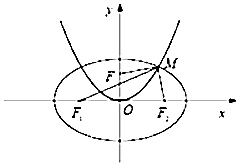
【题目】在平面直角坐标系xOy中,已知椭圆 ![]() +
+ ![]() =1(a>b>0)与双曲线
=1(a>b>0)与双曲线 ![]() ﹣y2=1有相同的焦点F1 , F2 , 抛物线x2=2py(p>0)的焦点为F,且与椭圆在第一象限的交点为M,若|MF1|+|MF2|=2
﹣y2=1有相同的焦点F1 , F2 , 抛物线x2=2py(p>0)的焦点为F,且与椭圆在第一象限的交点为M,若|MF1|+|MF2|=2 ![]() .
.
(1)求椭圆的方程;
(2)若|MF|= ![]() ,求抛物线的方程.
,求抛物线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有“今有五人分无钱,令上二人所得与下三人等,问各得几何?”.其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”这个问题中,甲所得为( )
A.![]() 钱
钱
B.![]() 钱
钱
C.![]() 钱
钱
D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() :对任意的
:对任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)求证![]() ;
;
(Ⅲ)若![]() ,求数集
,求数集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com