
在数列{ }中,已知
}中,已知

(1)求 并由此猜想数列{
并由此猜想数列{ }的通项公式
}的通项公式 的表达式;
的表达式;
(2)用数学归纳法证明你的猜想。
(1)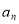 =
=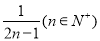 ; (2)见解析
; (2)见解析
【解析】
试题分析:(1)根据数列的递推公式不难求出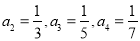 ,由前四项的共同特征可归纳出通项公式
,由前四项的共同特征可归纳出通项公式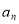 的表达式.
的表达式.
(2)根据数学归纳法的原理,证明分两步,第一,首先验证当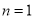 猜想正确;
猜想正确;
第二,在假设 时猜想正确的前提下,证明当
时猜想正确的前提下,证明当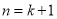 时猜想也正确;由此可下结论对任何
时猜想也正确;由此可下结论对任何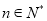 ,(1)中的猜想总是正确的.
,(1)中的猜想总是正确的.
试题解析:【解析】
(1)因为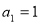 ,
,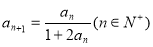
所以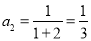 1分
1分
 2分
2分
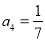 3分
3分
由此猜想数列{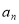 }的通项公式
}的通项公式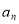 =
= 4分
4分
(2)下面用数学归纳法证明
①当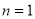 时,
时,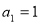 ,猜想成立 5分
,猜想成立 5分
②假设当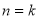 时,猜想成立,即
时,猜想成立,即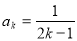
那么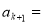
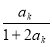 =
=
 10分
10分
即当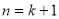 时,命题成立 11分
时,命题成立 11分
综合①②可知,猜想成立。 12分
考点:1、数列的递推公式;2、用数学归纳法证明与正整数有关的命题.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源:2015届江西赣州六校高二上学期期末联考文科数学试卷(解析版) 题型:选择题
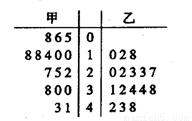
从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为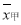 ,
,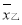 ,中位数分别为
,中位数分别为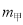 ,
,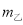 ,则( )
,则( )
A.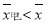 ,
,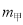

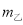 B.
B.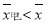 ,
,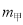
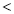
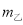
C.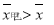 ,
,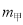

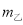 D.
D.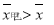 ,
,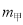
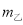
查看答案和解析>>
科目:高中数学 来源:2015届江西新余市高二上学期期末理科A数学试卷(解析版) 题型:选择题
已知数列 满足:
满足: ,
, ,若
,若 ,
, ,且数列
,且数列 的单调递增数列,则实数
的单调递增数列,则实数 的取值范围为( )
的取值范围为( )
A. B.
B.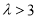 C.
C. D.
D.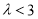
查看答案和解析>>
科目:高中数学 来源:2015届江西南昌市四校高二上学期期末联考文科数学试卷(解析版) 题型:选择题
如图,抛物线 的焦点为
的焦点为 ,准线为
,准线为 ,经过
,经过 且斜率为
且斜率为 的直线与抛物线在
的直线与抛物线在 轴上方的部分相交于点
轴上方的部分相交于点 ,
, ,垂足为
,垂足为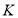 ,则
,则 的面积是( )
的面积是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com