
已知二次函数 .
.
(1)若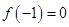 ,试判断函数
,试判断函数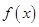 零点个数;
零点个数;
(2)是否存在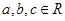 ,使
,使 同时满足以下条件
同时满足以下条件
①对任意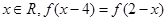 ,且
,且 ;
;
②对任意 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(3)若对任意 且
且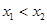 ,
, ,试证明存在
,试证明存在 ,
,
使 成立。
成立。
(1)函数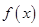 有两个零点。(2)当
有两个零点。(2)当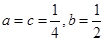 时,
时,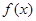 同时满足条件①、②. (3)利用零点存在性定理证明即可
同时满足条件①、②. (3)利用零点存在性定理证明即可
【解析】
试题分析:(1)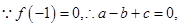
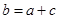
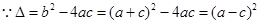 当
当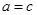 时
时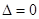 ,
,
函数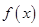 有一个零点; 3分
有一个零点; 3分
当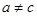 时,
时,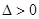 ,函数
,函数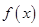 有两个零点。 5分
有两个零点。 5分
(2)假设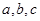 存在,由①知抛物线的对称轴为x=-1,
存在,由①知抛物线的对称轴为x=-1,
∴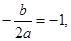 即
即 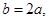 7分
7分
由②知对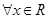 ,都有
,都有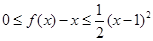
令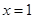 得
得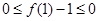

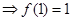
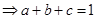 又因为
又因为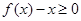 恒成立,
恒成立,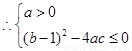
 ,即
,即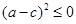 ,即
,即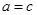
由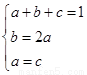 得
得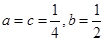 , 10分
, 10分
当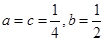 时,
时,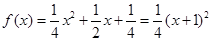 ,
,
其顶点为(-1,0)满足条件①,又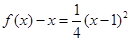
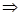 对
对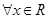 ,
,
都有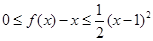 ,满足条件②.
,满足条件②.
∴存在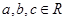 ,使
,使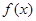 同时满足条件①、②. .12分
同时满足条件①、②. .12分
(3)令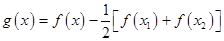 ,则
,则
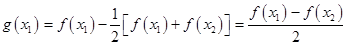
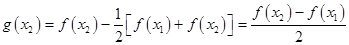 ,
,
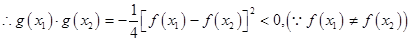
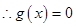 在
在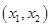 内必有一个实根。即
内必有一个实根。即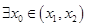 ,
,
使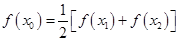 成立 18分
成立 18分
考点:本题考查了函数的零点及恒成立问题
点评:①二次函数、一元二次方程和一元二次不等式是一个有机的整体,也是高考热点,要深刻理解它们相互之间的关系,能用函数思想来研究方程和不等式,便是抓住了关键.②二次函数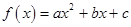 的图像形状、对称轴、顶点坐标、开口方向等是处理二次函数问题的重要依据.
的图像形状、对称轴、顶点坐标、开口方向等是处理二次函数问题的重要依据.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
已知二次函数![]() ,
,
(1)当![]() 时,
时,![]() 在 [ – 1,1 ] 上的最大值为
在 [ – 1,1 ] 上的最大值为![]() ,求
,求![]() 的最小值;
的最小值;
(2)对于任意的![]() ,总有
,总有![]() ,求a的取值范围;
,求a的取值范围;
(3)若当![]() 时,记
时,记![]() ,令a = 1,求证:
,令a = 1,求证:![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修2-2 1.2导数的运算练习卷(解析版) 题型:选择题
已知二次函数 在x=1处的导数值为1,则该函数的最大值是 (
)
在x=1处的导数值为1,则该函数的最大值是 (
)
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2010年江西省高一上学期期中考试数学卷 题型:解答题
(本小题12分) 已知二次函数 。
。
(1)指出图像的开口方向、对称轴方程、顶点坐标;
(2)画出它的图像,并说明其图像由 的图像经过怎样平移得来;
的图像经过怎样平移得来;
(3)求函数的最大值或最小值;
(4)写出函数的单调区间(不必证明)。

查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试12-理科-算法、复数、推理与证明 题型:解答题
已知二次函数 .
.
(1)若 ,试判断函数
,试判断函数 零点个数;
零点个数;
(2)若对 且
且 ,
, ,试证明
,试证明 ,使
,使
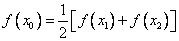 成立。
成立。
(3)是否存在 ,使
,使 同时满足以下条件①对
同时满足以下条件①对 ,且
,且 ;②对
;②对 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com