
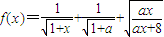 ,x∈(0,+∞).
,x∈(0,+∞). ,则abx=8①,
,则abx=8①, ②,将f(x)解析式进行放缩,使用基本不等式,可证
②,将f(x)解析式进行放缩,使用基本不等式,可证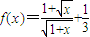 ,求得
,求得 ,
, ,
,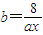 ,则abx=8①,
,则abx=8①, ②
②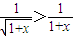 ,
, ,
, ,
,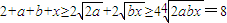 ,得a+b+x≥6.
,得a+b+x≥6.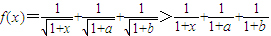


 .
.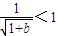 ,
,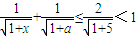 ,此时
,此时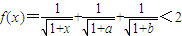 .
.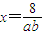 ,
, ,
,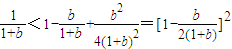
 ④
④ ⑤,
⑤,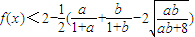 ⑥
⑥ ⑦,
⑦,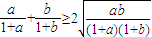 ,
, ,即ab+8>(1+a)(1+b),也即a+b<7,据③,此为显然.
,即ab+8>(1+a)(1+b),也即a+b<7,据③,此为显然.

 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年周至二中三模理) 已知函数f (x)(0≤x≤1)的图象的一段圆弧(如图所示)若![]() ,则 ( )
,则 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)前三个判断都不正确
(D)前三个判断都不正确

查看答案和解析>>
科目:高中数学 来源: 题型:
(14分)已知函数![]() ,( x>0).
,( x>0).
(I)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(II)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ma,mb]
(m≠0),求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com