
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的定义域;
的定义域;
(2)试判断函数![]() 在区间
在区间![]() 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)若![]() 在区间
在区间![]() 上恒取正值,求实数
上恒取正值,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)函数
;(2)函数![]() 在区间
在区间![]() 上是减函数,证明见解析;(3)
上是减函数,证明见解析;(3)![]()
【解析】
(1)将![]() 代入得到
代入得到![]() 的解析式,根据解析式要有意义,列出不等式,求解即可得到
的解析式,根据解析式要有意义,列出不等式,求解即可得到![]() 的定义域;
的定义域;
(2)利用函数单调性的定义,令![]() ,先判断出
,先判断出![]() ,再根据对数的单调性,判断出
,再根据对数的单调性,判断出![]() ,从而证明结结论;
,从而证明结结论;
(3)将![]() 在
在![]() 上恒取正值,等价为
上恒取正值,等价为![]() 在
在![]() 上恒成立,转化为
上恒成立,转化为![]() ,利用
,利用![]() 的单调性即可求出
的单调性即可求出![]() 的最小值,从而列出不等式,求解即可得到
的最小值,从而列出不等式,求解即可得到![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,
,![]() ,即
,即![]() ,
,![]() ,即
,即![]() ,
,
∴函数![]() 的定义域为
的定义域为![]() ;
;
(2)函数![]() 在区间
在区间![]() 上是减函数.
上是减函数.
证明:任取![]() ,且
,且![]() ,
,![]() ,
,
令![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上是减函数;
上是减函数;
(3)由(2)可知,![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() 在
在![]() 上是单调递减函数,
上是单调递减函数,
∴![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
∵![]() 在
在![]() 上恒取正值,即
上恒取正值,即![]() 在
在![]() 上恒成立,
上恒成立,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() 的取值范围为
的取值范围为![]() .
.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
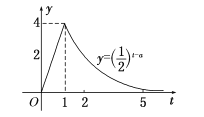
(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 、
、![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 和曲线
和曲线![]() 只有一个交点,求
只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,所得图象对应的函数为
个单位后,所得图象对应的函数为![]() .若关于
.若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率都为50%,现采用随机模拟的方法估计该运动员四次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1,2,3,4表示命中,5,6,7,8 9表示不命中;再以每四个随机数为一组,代表四次投篮的结果.经随机模拟产生了20组随机数:9075 9660 1918 9257 2716 9325 8121 4589 5690 6832 4315 2573 3937 9279 5563 4882 7358 1135 1587 4989
据此估计,该运动员四次投篮恰有两次命中的概率为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com