
【题目】F1,F2是椭圆C1和双曲线C2的公共焦点,e1,e2分别为曲线C1,C2的离心率,P为曲线C1,C2的一个公共点,若![]() ,且
,且![]() ,则e1∈_____.
,则e1∈_____.
科目:高中数学 来源: 题型:
【题目】已知平面![]() ,直线
,直线![]() .给出下列命题:
.给出下列命题:
① 若![]() ,则
,则![]() ; ② 若
; ② 若![]() ,则
,则![]() ;
;
③ 若![]() ,则
,则![]() ; ④ 若
; ④ 若![]() ,则
,则![]() .
.
其中是真命题的是_________.(填写所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,首项a1=1,且a3+1是a2+1与a4+2的等比中项.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的五面体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 是正方形,二面角
是正方形,二面角![]() 的大小为
的大小为![]() .
.
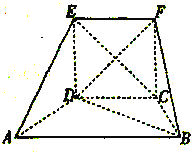
(1)在线段![]() 上找出一点
上找出一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() ,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若
,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若![]() OMN为直角三角形,则|MN|=
OMN为直角三角形,则|MN|=
A. ![]() B. 3 C.
B. 3 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上的三点![]() 、
、![]() 、
、![]() .
.
(1)求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的椭圆的标准方程;
的椭圆的标准方程;
(2)设点![]() 、
、![]() 、
、![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() 、
、![]() 、
、![]() ,求以
,求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的双曲线的标准方程.
的双曲线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动.在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,
的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,过点
中,过点![]() 的直线与线段
的直线与线段![]() 分别相交于点
分别相交于点![]() ,若
,若![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)定义函数![]() ,点列
,点列![]() 在函数
在函数![]() 的图像上,且数列
的图像上,且数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列,
为公比的等比数列,![]() 为原点,令
为原点,令![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
(3)设函数![]() 为
为![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() 函数
函数![]() 的图像关于直线
的图像关于直线![]() 对称,当方程
对称,当方程![]() 在
在![]() 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com