
 与双曲线
与双曲线 -y2=1有公共焦点,且离心率为
-y2=1有公共焦点,且离心率为 .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x=
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x= 分别交于M,N两点.
分别交于M,N两点. ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.
 ,利用PS⊥AM,由射影定理可得MS2=MB•MP.
,利用PS⊥AM,由射影定理可得MS2=MB•MP. ,只须T到直线BS的距离等于
,只须T到直线BS的距离等于 ,由此问题转化为研究与直线SB平行且距离为
,由此问题转化为研究与直线SB平行且距离为 的直线与椭圆的交点个数问题.
的直线与椭圆的交点个数问题. 与双曲线
与双曲线 -y2=1有公共焦点
-y2=1有公共焦点 ,
, ,
, ,
, .…(3分)
.…(3分)
 得(1+4k2)x2+16k2x+16k2-4=0
得(1+4k2)x2+16k2x+16k2-4=0 得
得 ,从而
,从而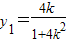 …(5分)
…(5分)
 ,
,
 ,
, ,
, 得
得


 ,即
,即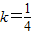 时等号成立
时等号成立 时,线段MN的长度取最小值
时,线段MN的长度取最小值
 ,∴
,∴ …(9分)
…(9分) ,只须T到直线BS的距离等于
,只须T到直线BS的距离等于 ,
, 的直线l'上.
的直线l'上.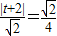 ,解得
,解得 或
或 .
. 时,由
时,由 ,得5x2-12x+5=0
,得5x2-12x+5=0 时,由
时,由 得5x2-20x+21=0,
得5x2-20x+21=0, .…(12分)
.…(12分)

科目:高中数学 来源:湖南省师大附中2011-2012学年度高二上学期期中考试数学理科试题(人教版) 题型:044
已知椭圆C:![]() 与双曲线
与双曲线![]() 有公共焦点,且离心率为
有公共焦点,且离心率为![]() .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:![]() 分别交于M,N两点.
分别交于M,N两点.
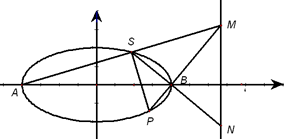
(1)求椭圆C的方程;
(2)延长MB交椭圆C于点P,若PS⊥AM,试证明MS2=MB·MP.
(3)当线段MN的长度最小时,在椭圆C上是否存在点T,使得△TSB的面积为![]() ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三第一次月考文科数学试卷(解析版) 题型:选择题
已知椭圆C1: 与双曲线C2:
与双曲线C2: 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( )
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:
已知椭圆C: 与双曲线
与双曲线 -y2=1有公共焦点,且离心率为
-y2=1有公共焦点,且离心率为 .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x=
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x= 分别交于M,N两点.
分别交于M,N两点. ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南师大附中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
 与双曲线
与双曲线 -y2=1有公共焦点,且离心率为
-y2=1有公共焦点,且离心率为 .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x=
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:x= 分别交于M,N两点.
分别交于M,N两点. ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com