高一某个研究性学习小组进行市场调查,某生活用品在过去100天的销售量和价格均为时间t的函数,且销售量近似地满足g(t)=-t+110(1≤t≤100),t∈N.前40天的价格为f(t)=t+8(1≤t≤40),后60天的价格为f(t)=-0.5t+69(41≤t≤100).
(1)试写出该种生活用品的日销售额S与时间t的函数关系式;
(2)试问在过去100天中是否存在最高销售额,是哪天?
解:(1)由题意,S=g(t)•f(t)=
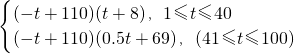
=
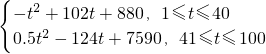
(2)当1≤t≤40时,S=-t
2+102t+880=-(t-51)
2+880+51
2,
在[1,40]上为增函数,∴当t=40时,S
max=-40
2+102×40+880=3360;
当41≤t≤100时,S=0.5t
2-124t+7 590=0.5(t-124)
2+7590-

×124
2,
在[41,100]上函数为减函数,
∴t=41时,S
max=41
2×0.5-124×41+7 590=3346.5.
∴在过去100天中第40天的销售额最高,最高值为3360元.
分析:(1)利用S=g(t)•f(t),即可得到函数解析式;
(2)利用配方法,结合函数的单调性,分段求最值,即可得到结论.
点评:本题考查函数模型的建立,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

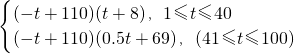
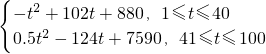
 ×1242,
×1242,

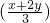
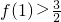 ,写出一个满足上述条件的解析式;并证明此函数f(x)∈A.
,写出一个满足上述条件的解析式;并证明此函数f(x)∈A.