
【题目】2019年春节期间,某超市准备举办一次有奖促销活动,若顾客一次消费达到400元则可参加一次抽奖活动,超市设计了两种抽奖方案.
方案一:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得60元的返金券,若抽到白球则获得20元的返金券,且顾客有放回地抽取3次.
方案二:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得80元的返金券,若抽到白球则未中奖,且顾客有放回地抽取3次.
(1)现有两位顾客均获得抽奖机会,且都按方案一抽奖,试求这两位顾客均获得180元返金券的概率;
(2)若某顾客获得抽奖机会.
①试分别计算他选择两种抽奖方案最终获得返金券的数学期望;
②为了吸引顾客消费,让顾客获得更多金额的返金券,该超市应选择哪一种抽奖方案进行促销活动?
【答案】(1)![]() (2)①
(2)①![]() ②第一种抽奖方案.
②第一种抽奖方案.
【解析】
(1)方案一中每一次摸到红球的概率为![]() ,每名顾客有放回的抽3次获180元返金劵的概率为
,每名顾客有放回的抽3次获180元返金劵的概率为![]() ,根据相互独立事件的概率可知两顾客都获得180元返金劵的概率
,根据相互独立事件的概率可知两顾客都获得180元返金劵的概率
(2)①分别计算方案一,方案二顾客获返金卷的期望,方案一列出分布列计算即可,方案二根据二项分布计算期望即可 ②根据①得出结论.
(1)选择方案一,则每一次摸到红球的概率为![]()
设“每位顾客获得180元返金劵”为事件A,则![]()
所以两位顾客均获得180元返金劵的概率![]()
(2)①若选择抽奖方案一,则每一次摸到红球的概率为![]() ,每一次摸到白球的概率为
,每一次摸到白球的概率为![]() .
.
设获得返金劵金额为![]() 元,则
元,则![]() 可能的取值为60,100,140,180.
可能的取值为60,100,140,180.
则![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
所以选择抽奖方案一,该顾客获得返金劵金额的数学期望为
![]() (元)
(元)
若选择抽奖方案二,设三次摸球的过程中,摸到红球的次数为![]() ,最终获得返金劵的金额为
,最终获得返金劵的金额为![]() 元,则
元,则![]() ,故
,故![]()
所以选择抽奖方案二,该顾客获得返金劵金额的
数学期望为![]() (元).
(元).
②即![]() ,所以该超市应选择第一种抽奖方案
,所以该超市应选择第一种抽奖方案


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知圆C经过点![]() ,
,![]() 两点,且圆心C在直线
两点,且圆心C在直线![]() 上.
上.
(1)求圆C的方程;
(2)设![]() ,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使
,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使![]() 是常数,若存在,求出点N坐标;若不存在,说明理由.
是常数,若存在,求出点N坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是y=f(x)导函数的图象,对于下列四个判断:
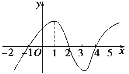
①f(x)在[-2,-1]上是增函数;
②x=-1是f(x)的极小值点;
③f(x)在[-1,2]上是增函数,在[2,4]上是减函数;
④x=3是f(x)的极小值点.
其中判断正确的是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口的水深![]() (米)是时间
(米)是时间![]() (
(![]() ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过长期观测,![]() 可近似的看成是函数
可近似的看成是函数![]()
(1)根据以上数据,求出![]() 的解析式;
的解析式;
(2)若船舶航行时,水深至少要![]() 米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级参加期末考试的学生中抽出60名,其成绩(均为整数)的频率分布直方图如图所示,由此估计此次考试成绩的中位数、众数分别是( )
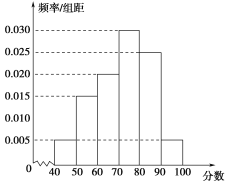
A.73.3,75B.73.3,80
C.70,70D.70, 75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,当直线
,当直线![]() 的倾斜角是
的倾斜角是![]() 时,
时, ![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() .
.

(1)求![]() 的值;
的值;
(2)以![]() 为直径的圆交
为直径的圆交![]() 轴于点
轴于点![]() ,记劣弧
,记劣弧![]() 的长度为
的长度为![]() ,当直线
,当直线![]() 绕
绕![]() 点旋转时,求
点旋转时,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com