
(文科做)(本题满分14分)如图,在长方体
ABCD—A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1—EC-D的大小为 .
. 
(理科做)(本题满分14分)
如图,在直三棱柱ABC – A1B1C1中,∠ACB = 90°,CB = 1,
CA = ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.
(Ⅰ)求证:AM⊥平面A1BC;
(Ⅱ)求二面角B – AM – C的大小;
(Ⅲ)求点C到平面ABM的距离.
、(文)解法一(1)∵AE⊥平面AA1DD1,A1D⊥AD1,∴D1E⊥A1D.
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1= ,AD1=
,AD1= ,故
,故
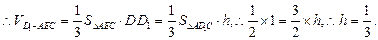
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,∴∠DHD1为二面角D1—EC—D的平面角.设AE=x,则BE=2-x,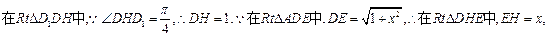

 (3)设平面D1EC的法向量
(3)设平面D1EC的法向量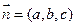 ,
,
由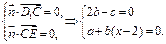 令b="1," ∴c=2,a=2-x,∴
令b="1," ∴c=2,a=2-x,∴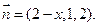 依题意
依题意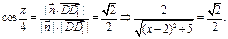 ∴
∴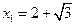 (不合,舍去),
(不合,舍去), ∴AE=
∴AE= 时,二面角D1—EC—D的大小为
时,二面角D1—EC—D的大小为 .
.  (Ⅲ)设点C到平面ABM的距离为h,易知BO =
(Ⅲ)设点C到平面ABM的距离为h,易知BO =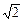 ,可知S△ABM =
,可知S△ABM = · AM · BO =
· AM · BO = ×
× ∵VC – ABM = VM – ABC ∴
∵VC – ABM = VM – ABC ∴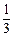 hS△ABM =
hS△ABM =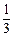 MC ·S△ABC
MC ·S△ABC
∴h =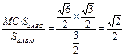 ∴点C到平面ABM的距离为
∴点C到平面ABM的距离为 解法二:(Ⅰ)同解法一
解法二:(Ⅰ)同解法一
(Ⅱ)如图以C为原点,CA,CB,CC1所在直线
分别为x轴,y轴,z轴,建立空间直角坐标系,
则A ( ,0,0),A1(
,0,0),A1( ,0,
,0, ),B (0,1,0),
),B (0,1,0),
设M (0,0,z1) ∵AM⊥BA1.
∴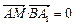 ,即– 3 + 0 +
,即– 3 + 0 + z1 = 0,故z1 =
z1 = 0,故z1 = ,所以M (0,0,
,所以M (0,0, )
)
设向量m = (x,y,z)为平面AMB的法向量,则m⊥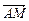 ,m⊥
,m⊥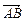 ,则
,则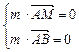 即
即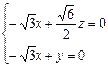 ,令x = 1,平面AMB的一个法向量为m = (1,
,令x = 1,平面AMB的一个法向量为m = (1, ,
,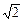 ),显然向量
),显然向量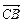 是平面AMC的一个法向量
是平面AMC的一个法向量
cos < m, ,易知,m与
,易知,m与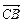 所夹的角等于二面角B—AM—C的大小,故所求二面角的大小为45°.(Ⅲ)所求距离为:
所夹的角等于二面角B—AM—C的大小,故所求二面角的大小为45°.(Ⅲ)所求距离为: , 即点C到平面ABM的距离为
, 即点C到平面ABM的距离为
解析


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
如图,正 的中线
的中线 与中位线
与中位线 相交
相交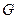 ,
,
已知 是
是 绕
绕 旋转过程中的一个
旋转过程中的一个
图形( 不与
不与 重合).现给出下列四个命题:
重合).现给出下列四个命题:
①动点 在平面
在平面 上的射影在线段
上的射影在线段 上;
上;
②平面 平面
平面 ;
;
③三棱锥 的体积有最大值;
的体积有最大值;
④异面直线 与
与 不可能垂直.其中正确的命题的序号是_________.
不可能垂直.其中正确的命题的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在60°的二面角的棱上有A,B两点,线段AC,BD分别在二面角的两个面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长度为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com