
【题目】【2018届江西省南昌市高三第一轮】已知![]() 分别为
分别为![]() 三个内角
三个内角![]() 的对边,且
的对边,且![]() .
.
(Ⅰ)求![]() ;
;
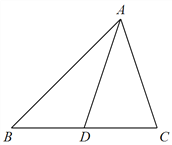
(Ⅱ)若![]() 为
为![]() 边上的中线,
边上的中线, ![]() ,
, ![]() ,求
,求![]() 的面积.
的面积.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析: (1)由正弦定理化简已知的式子,由内角和定理、诱导公式、两角和差的正弦公式化简后,由内角的范围和特殊角的三角函数值求出A;(2)由题意和平方关系求出sinB,由内角和定理、诱导公式、两角和的正弦公式求出sinC,由正弦定理求出a和c关系,根据题意和余弦定理列出方程,代入数据求出a、c,由三角形的面积公式求出答案.
解析:
(Ⅰ)∵![]() ,由正弦定理得:
,由正弦定理得:
![]() ,即
,即
![]() ,化简得:
,化简得: ![]() ,∴
,∴![]() .在
.在![]() 中,
中, ![]() ,∴
,∴![]() ,得
,得![]() .
.
(Ⅱ)在![]() 中,
中, ![]() ,得
,得![]() ,
,
则![]()
![]() ,由正弦定理得
,由正弦定理得![]() .
.
设![]() ,在
,在![]() 中,由余弦定理得:
中,由余弦定理得: ![]() ,
,
则![]() ,解得
,解得![]() ,即
,即![]() ,
,
故![]() .
.
点睛: 本题考查了正弦定理、余弦定理,三角形的面积公式,以及两角和差的正弦公式等,注意内角的范围,考查化简、变形、计算能力.注意当已知三角形的一个边和两个角时,用正弦定理.已知两角一对边时,用正弦定理,已知两边和对角时用正弦较多.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (其中e是自然对数的底数,常数a>0).
(其中e是自然对数的底数,常数a>0).
(1)当a=1时,求曲线在(0,f(0))处的切线方程;
(2)若存在实数x∈(a,2],使得不等式f(x)≤e2成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,过
,过![]() 且与
且与![]() 轴垂直的直线与椭圆
轴垂直的直线与椭圆![]() 在第一象限内的交点为
在第一象限内的交点为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当
两点,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点O,左焦点为F1(-1,0)的椭圆C的左顶点为A,上顶点为B,F1到直线AB的距离为![]() |OB|.
|OB|.
(1)求椭圆C的方程;
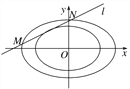
(2)如图,若椭圆![]() ,椭圆
,椭圆![]() ,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)e-x(e为自然对数的底数).
(1)求函数f(x)的单调区间;
(2)设函数φ(x)=xf(x)+tf′(x)+e-x,存在实数x1,x2∈[0,1],使得2φ(x1)<φ(x2)成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 的中点,过点
的中点,过点![]() 的平面
的平面![]() 与平面
与平面![]() 平行,且与长方体的面相交,交线围成一个几何图形.
平行,且与长方体的面相交,交线围成一个几何图形.
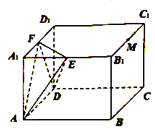
(1)在图中画出这个几何图形(说明画法,不需要说明理由);
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把2支相同的晨光签字笔,3支相同英雄钢笔全部分给4名优秀学生,每名学生至少1支,则不同的分法有( )
A. 24种 B. 28种 C. 32种 D. 36种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com