
【题目】设数列{an}的前n项和为Sn , 若 ![]() (n∈N*),则称{an}是“紧密数列”;
(n∈N*),则称{an}是“紧密数列”;
(1)若a1=1, ![]() ,a3=x,a4=4,求x的取值范围;
,a3=x,a4=4,求x的取值范围;
(2)若{an}为等差数列,首项a1 , 公差d,且0<d≤a1 , 判断{an}是否为“紧密数列”;
(3)设数列{an}是公比为q的等比数列,若数列{an}与{Sn}都是“紧密数列”,求q的取值范围.
【答案】
(1)解:由题意, ![]() 且
且 ![]() ,∴2≤x≤3,
,∴2≤x≤3,
∴x的取值范围是[2,3];
(2)解:由题意,an=a1+(n﹣1)d,∴ ![]() ,
,
![]() 随着n的增大而减小,所以当n=1时,
随着n的增大而减小,所以当n=1时, ![]() 取得最大值,∴
取得最大值,∴ ![]() ≤2,
≤2,
∴{an}是“紧密数列”;
(3)解:由题意得,等比数列{an}的公比q
当q≠1时,所以an=a1qn﹣1,Sn= ![]() ,
, ![]() ,
,
因为数列{an}与{Sn}都是“紧密数列”,所以 ![]() ,
, ![]() ,解得
,解得 ![]() ,
,
当q=1时,an=a1,Sn=na1,则 ![]() =1,
=1, ![]() ,符合题意,
,符合题意,
∴q的取值范围是 ![]() .
.
【解析】(1)由题意, ![]() 且
且 ![]() ,即可求出x的取值范围;(2)由题意,an=a1+(n﹣1)d,
,即可求出x的取值范围;(2)由题意,an=a1+(n﹣1)d, ![]() ,根据“紧密数列”的定义即可证明结论;(3)先设公比是q并判断出q≠1,由等比数列的通项公式、前n项和公式化简
,根据“紧密数列”的定义即可证明结论;(3)先设公比是q并判断出q≠1,由等比数列的通项公式、前n项和公式化简 ![]() ,根据“紧密数列”的定义列出不等式组,再求出公比q的取值范围.
,根据“紧密数列”的定义列出不等式组,再求出公比q的取值范围.


科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1BlC1中,平面α与棱AB,AC,A1C1 , A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过C(1,-1),D(-1,1)两点,且圆心M在x+y-2=0上.
(1)求圆M的方程;
(2)设点P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点; 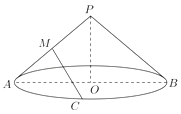
(1)求三棱锥P﹣ACO的体积;
(2)求异面直线MC与PO所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点.求异面直线A1E与GF所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com