【答案】
分析:先由
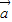
⊥(
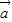
+
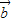
)?
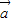
•(
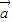
+
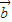
)=0,求出
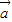
•
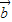
的值,然后根据公式cos<
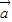
,
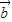
>=
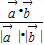
求出它们夹角的余弦值,最后利用特殊角三角函数值求得夹角.
解答:解:因为
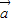
⊥(
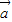
+
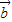
),所以
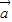
(
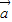
+
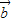
)=0,整理得
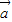
•
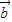
=-
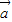 2
2=-1,
所以cos<
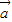
,
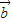
>=
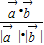
=-

所以
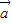
与
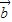
夹角为120°.
故答案为120°.
点评:向量夹角问题的解决:一般把公式cos<
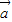
,
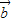
>=
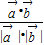
作为问题的切入点,然后通过条件计算
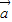
•
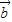
的值.
练习册系列答案
相关习题
科目:高中数学
来源:2013-2014学年山东省等四校高三上学期期中联考理科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2014届湖北襄阳四中、龙泉中学、荆州中学高三10月联考理数学卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2014届天津市高三第一次六校联考文科数学试卷(解析版)
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省济南外国语学校高二(上)入学考试数学试卷 (解析版)
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2009-2010学年数学寒假作业(07)(解析版)
题型:填空题
查看答案和解析>>

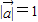 ,
, ,
,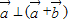 ,则
,则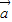 与
与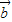 夹角的度数为 .
夹角的度数为 .  阅读快车系列答案
阅读快车系列答案