
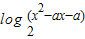 的值域是R,且在(-∞,1-
的值域是R,且在(-∞,1-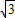 )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.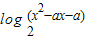 中,令t=x2-ax-a;根据题意,若函数y=
中,令t=x2-ax-a;根据题意,若函数y=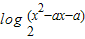 的值域是R,则t的最小值必然小于或等于0,则可得a2+4a≥0,又由f(x)在(-∞,1-
的值域是R,则t的最小值必然小于或等于0,则可得a2+4a≥0,又由f(x)在(-∞,1-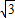 )上是减函数,则有
)上是减函数,则有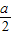 ≤1-
≤1-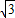 ,且t(1-
,且t(1-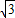 )>0,综合三个式子可得不等式组,解可得答案.
)>0,综合三个式子可得不等式组,解可得答案.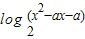 中,令t=x2-ax-a,则y=log2t;
中,令t=x2-ax-a,则y=log2t;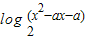 的值域是R,则二次函数t=x2-ax-a的最小值小于等于0,有a2+4a≥0,
的值域是R,则二次函数t=x2-ax-a的最小值小于等于0,有a2+4a≥0,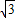 )上是减函数,有
)上是减函数,有 ≥1-
≥1-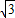 ,且t(1-
,且t(1-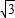 )>0,
)>0, ,解可得0≤a<2;
,解可得0≤a<2;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年吉林省松原市油田高中高三(上)第二次摸底数学试卷(理科)(解析版) 题型:填空题
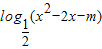 的值域为R;
的值域为R;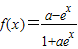 在定义域上是奇函数”的充分不必要条件.
在定义域上是奇函数”的充分不必要条件.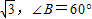 ,AB=1的三角形△ABC有两个.
,AB=1的三角形△ABC有两个.查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省松原市油田高中高三(上)第二次摸底数学试卷(文科)(解析版) 题型:填空题
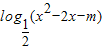 的值域为R;
的值域为R;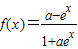 在定义域上是奇函数”的充分不必要条件.
在定义域上是奇函数”的充分不必要条件.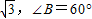 ,AB=1的三角形△ABC有两个.
,AB=1的三角形△ABC有两个.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省六安市寿县二中高三(上)月考数学试卷(解析版) 题型:填空题
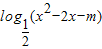 的值域为R;
的值域为R;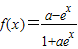 在定义域上是奇函数”的充分不必要条件.
在定义域上是奇函数”的充分不必要条件.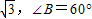 ,AB=1的三角形△ABC有两个.
,AB=1的三角形△ABC有两个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com