
【题目】设函数f(x)=sinxcosx将 f(x)的图象向右平移 ![]() (0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x=
(0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x= ![]() .
.
(1)求φ;
(2)求函数y=g(x)的单调增区间.
【答案】
(1)解:f(x)= ![]() sin2x,g(x)=
sin2x,g(x)= ![]() sin(2x﹣φ)
sin(2x﹣φ)
∵x= ![]() 是函数y=g(x)图象的对称轴.
是函数y=g(x)图象的对称轴.
∴sin(2× ![]() ﹣φ)=±1,
﹣φ)=±1, ![]() ﹣φ=kπ+
﹣φ=kπ+ ![]() ,k∈Z.
,k∈Z.
∵0<φ<π,∴φ= ![]()
(2)解:由(1)知φ= ![]() ,因此y=sin(2x﹣
,因此y=sin(2x﹣ ![]() ).
).
由题意得2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z.
,k∈Z.
∴函数y=sin(2x﹣ ![]() )的单调增区间为[kπ+
)的单调增区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
【解析】(1)由已知利用平移变换规律可求g(x)= ![]() sin(2x﹣φ),由sin(2×
sin(2x﹣φ),由sin(2× ![]() ﹣φ)=±1,可求
﹣φ)=±1,可求 ![]() ﹣φ=kπ+
﹣φ=kπ+ ![]() ,k∈Z,结合范围0<φ<π,即可得解φ的值.(2)由2kπ﹣
,k∈Z,结合范围0<φ<π,即可得解φ的值.(2)由2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,即可解得函数y=sin(2x﹣
,k∈Z,即可解得函数y=sin(2x﹣ ![]() )的单调增区间.
)的单调增区间.
【考点精析】掌握函数y=Asin(ωx+φ)的图象变换是解答本题的根本,需要知道图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点![]() 在正视图中所示位置:
在正视图中所示位置:![]() 为所在线段中点,
为所在线段中点,![]() 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从![]() 点到
点到![]() 点的最短路径的长.
点的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
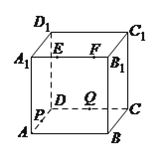
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,动点
,动点![]() 、
、![]() 在棱
在棱![]() 上,动点
上,动点![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上,若
上,若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() 大于零),则四面体
大于零),则四面体![]() 的体积( ).
的体积( ).
A. 与![]() ,
,![]() ,
,![]() 都有关 B. 与
都有关 B. 与![]() 有关,与
有关,与![]() ,
,![]() 无关
无关
C. 与![]() 有关,与
有关,与![]() ,
,![]() 无关 D. 与
无关 D. 与![]() 有关,与
有关,与![]() ,
,![]() 无关
无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)若出现故障的机器台数为![]() ,求
,求![]() 的分布列;
的分布列;
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于![]() 为合格品,小于
为合格品,小于![]() 为次品.现随机抽取这种芯片共
为次品.现随机抽取这种芯片共![]() 件进行检测,检测结果统计如表:
件进行检测,检测结果统计如表:
测试指标 |
|
|
|
|
|
芯片数量(件) |
|
|
|
|
|
已知生产一件芯片,若是合格品可盈利![]() 元,若是次品则亏损
元,若是次品则亏损![]() 元.
元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产![]() 件芯片所获得的利润不少于
件芯片所获得的利润不少于![]() 元的概率.
元的概率.
(Ⅱ)记![]() 为生产
为生产![]() 件芯片所得的总利润,求随机变量
件芯片所得的总利润,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为1,
的棱长为1, ![]() 分别是棱
分别是棱![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() 交于
交于![]() ,设
,设![]() ,
, ![]() ,给出以下四个命题:
,给出以下四个命题:
①![]()
②当且仅当![]() 时,四边形
时,四边形![]() 的面积最小;
的面积最小;
③四边形![]() 周长
周长![]() ,
, ![]() ,则
,则![]() 是奇函数;
是奇函数;
④四棱锥![]() 的体积
的体积![]() 为常函数;
为常函数;
其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市共有初中学生270000人,其中初一年级,初二年级,初三年级学生人数分别为99000,90000,81000,为了解该市学生参加“开放性科学实验活动”的意向,现采用分层抽样的方法从中抽取一个容量为3000的样本,那么应该抽取初三年级的人数为( )
A.800
B.900
C.1000
D.1100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将五个1,五个2,五个3,五个4,五个5共25个数填入一个5行5列的表格内(每格填入一个数),使得同一行中任何两数之差的绝对值不超过2,考查每行中五个数之和,记这五个和的最小值为![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A. ![]() B. 9 C. 10 D. 11
B. 9 C. 10 D. 11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 、
、![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.
(Ⅰ)若点![]() 、
、![]() 分别是双曲线
分别是双曲线![]() 的虚轴、实轴的一个端点,试在平面上找两点
的虚轴、实轴的一个端点,试在平面上找两点![]() 、
、![]() ,使得双曲线
,使得双曲线![]() 上任意一点到
上任意一点到![]() 、
、![]() 这两点距离差的绝对值是定值.
这两点距离差的绝对值是定值.
(Ⅱ)若以原点![]() 为圆心的圆
为圆心的圆![]() 截直线
截直线![]() 所得弦长是
所得弦长是![]() ,求圆
,求圆![]() 的方程以及这条弦的中点.
的方程以及这条弦的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com