【题目】某电视台为宣传本省，随机对本省内15～65岁的人群抽取了
人，回答问题“本省内著名旅游景点有哪些”统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 |
|
|
|
第2组 |
| 18 |
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
（1）分别求出
的值；
（2）从第2、3、4组回答正确的人中用分层抽样的方法抽取6人，求第2、3、4组每组各抽取多少人？
（3）指出直方图中，这组数据的中位数是多少（取整数值）？
【答案】（1）
，
，
，
（2）第2组：
(人)；第3组：
(人)；第4组：
(人) （3）42
【解析】
（1）先算出第4组的总人数，再根据频率分布直方图得到第4组的频率，从而可计算总人数
，最后计算出相应组人数后利用统计结果表可得
的值.
（2）先算出第2、3、4组回答正确的总人数，再按比例抽取即可.
（3）根据频率分布直方图可知中位数
满足
，从而可得的近似值.
（1）由频率表中第4组数据可知，第4组总人数为
，
再结合频率分布直方图可知
，
，
，
，
.
（2）第2、3、4组回答正确的共有54人．
∴利用分层抽样在54人中抽取6人，每组分别抽取的人数为：
第2组：
(人)；
第3组：
(人)；
第4组：
(人)．
（3）设这组数据的中位数为，
由频率分布直方图可得前两组的频率之和为
，最后两组的频率之和为
，
故在第三组中，且
，解得
，故
.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】下列命题中正确的是（ ）
A. 命题
：
，
，则命题
：
，
B. “
”是“
”的充要条件
C. 命题“若
，则
或
”的逆否命题是“若
或
，则
”
D. 命题：，
；命题
：对，总有
；则
是真命题
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义在区间
上的函数
的图象关于直线
对称，当
时，函数
.
（1）求
，
的值；
（2）求的表达式；
（3）若关于
的方程
有解，那么将方程在
取某一确定值时所求得的所有解的和记为
，求的所有可能值及相应的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，港口
在港口
的正东120海里处，小岛
在港口的北偏东
的方向，且在港口北偏西
的方向上，一艘科学考察船从港口出发，沿北偏东的
方向以20海里/小时的速度驶离港口.一艘给养快艇从港口以60海里/小时的速度驶向小岛，在岛转运补给物资后以相同的航速送往科考船.已知两船同时出发，补给装船时间为1小时.
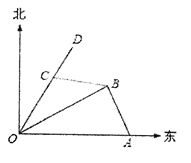
（1）求给养快艇从港口到小岛的航行时间；
（2）给养快艇驶离港口后，最少经过多少小时能和科考船相遇？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2019年，随着中国第一款5G手机投入市场，5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析，得到如下规律：每生产手机
万台，其总成本为
，其中固定成本为800万元，并且每生产1万台的生产成本为1000万元（总成本=固定成本+生产成本），销售收入
万元满足
（1）将利润
表示为产量
万台的函数；
（2）当产量为何值时，公司所获利润最大？最大利润为多少万元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知二次函数
满足
（
），且
．
（1）求
的解析式；
（2）若函数
在区间
上是单调函数，求实数
的取值范围；
（3）若关于
的方程
有区间
上有一个零点，求实数
的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
