
已知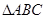 中,
中, ,
,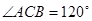 ,
,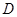 为
为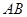 的中点,
的中点,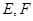 分别在线段
分别在线段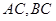 上,且
上,且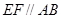
 交
交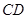 于
于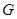 ,把
,把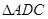 沿
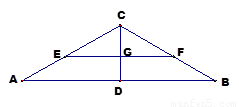
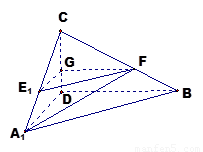
沿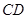 折起,如下图所示,
折起,如下图所示,

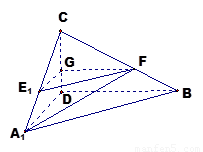
(1)求证: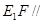 平面
平面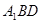 ;
;
(2)当二面角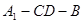 为直二面角时,是否存在点
为直二面角时,是否存在点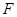 ,使得直线
,使得直线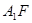 与平面
与平面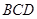 所成的角为
所成的角为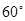 ,若存在求
,若存在求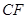 的长,若不存在说明理由.
的长,若不存在说明理由.
(1)证明 平面
平面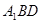 ,及
,及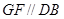 ,则
,则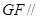 平面
平面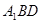 ,得到平面
,得到平面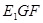 //平面
//平面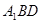 ,
,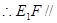 平面
平面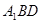 .
.
(2)存在点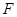 ,使得直线
,使得直线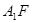 与平面
与平面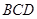 所成的角为
所成的角为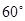 ,且
,且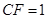 .
.
【解析】
试题分析:(1)证明“线面平行”,一般思路是通过证明“线线平行”或“面面平行”.本题中,注意到平面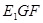 与平面
与平面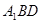 的平行关系易得,因此,通过证明“面面平行”,达到目的.
的平行关系易得,因此,通过证明“面面平行”,达到目的.
(2)存在性问题,往往通过“找,证”等,实现存在性的证明.本题从确定二面角的平面角入手,同时确定得到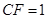 .
.
试题解析:(1)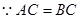 ,又
,又 为
为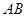 的中点
的中点
 ,又
,又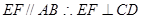 2分
2分
在空间几何体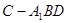 中,
中,
 ,则
,则 平面
平面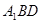
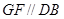 ,则
,则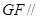 平面
平面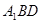
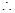 平面
平面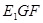 //平面
//平面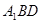 5分
5分
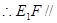 平面
平面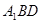 7分
7分
(2)∵二面角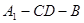 为直二面角,
为直二面角,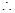 平面
平面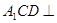 平面
平面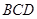
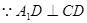 ,
,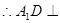 平面
平面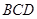 , 9分
, 9分
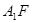 在平面
在平面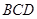 内的射影为
内的射影为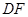 ,
,
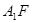 与平面
与平面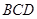 所成角为
所成角为 ,
,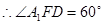 11分
11分
由于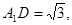
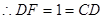 ,
,
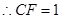 14分
14分
考点:平行关系,垂直关系,二面角.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源:2013-2014学年湖北黄冈中学、黄石二中、鄂州高中高三11月联考文数学试卷(解析版) 题型:解答题
已知 中,
中,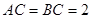 ,
, ,
,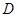 为
为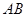 的中点,
的中点,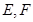 分别在线段
分别在线段 上的动点,且
上的动点,且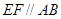 ,
, 交
交 于
于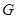 ,把
,把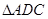 沿
沿 折起,如下图所示,
折起,如下图所示,
(Ⅰ)求证: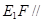 平面
平面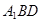 ;
;
(Ⅱ)当二面角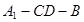 为直二面角时,是否存在点
为直二面角时,是否存在点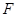 ,使得直线
,使得直线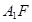 与平面
与平面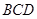 所成的角为
所成的角为 ,若存在求
,若存在求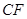 的长,若不存在说明理由。
的长,若不存在说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com