【题目】如图，某公园摩天轮的半径为
，圆心距地面的高度为
，摩天轮做匀速转动，每
转一圈，摩天轮上的点
的起始位置在最低点处.
（1）已知在时刻
时距离地面的高度
，（其中
），求
时距离地面的高度；
（2）当离地面
以上时，可以看到公园的全貌，求转一圈中有多少时间可以看到公园的全貌？
科目：高中数学 来源： 题型：
【题目】设某单位用2160万元购得一块空地，计划在该空地上建造一栋至少10层，每层2000平方米的楼房．经测算，如果将楼房建为
层，则每平方米的平均建筑费用为
(单位：元)．
(1)写出楼房每平方米的平均综合费用
关于建造层数
的函数关系式；
(2)该楼房应建造多少层时，可使楼房每平方米的平均综合费用最少？最少值是多少？
(注：平均综合费用＝平均建筑费用＋平均购地费用，平均购地费用＝
)
查看答案和解析>>
科目：高中数学 来源： 题型：
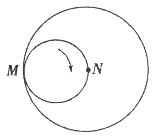
【题目】如图，一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动，M和N是小圆的一条固定直径的两个端点。那么，当小圆这样滚过大圆内壁的一周，点M，N在大圆内所绘出的图形大致是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设动点
是圆
上任意一点，过
作
轴的垂线，垂足为
，若点
在线段
上，且满足
．
（1）求点
的轨迹
的方程；
（2）设直线
与
交于
， 
两点，点
坐标为
，若直线
， 
的斜率之和为定值3，求证：直线
必经过定点，并求出该定点的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业生产甲乙两种产品，已知生产每吨甲产品要用A原料3吨，B原料2吨；生产每吨乙产品要用A原料1吨，B原料3吨，销售每吨甲产品可获得利润5万元，销售每吨乙产品可获得利润3万元。该企业在一个生产周期消耗A原料不超过13吨，B原料不超过18吨。问该企业如何安排可获得最大利润，最大利润是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出如下结论：
①函数
是奇函数；
②存在实数
，使得
；
③若
是第一象限角且
，则
；
④
是函数
的一条对称轴方程；
⑤函数
的图形关于点
成中心对称图形.
其中正确的结论的序号是__________．（填序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线顶点在原点，焦点在
轴上，又知此抛物线上一点
到焦点的距离为6．
（1）求此抛物线的方程；
（2）若此抛物线方程与直线
相交于不同的两点
、
，且
中点横坐标为2，求
的值．
【答案】（1）
；（2）2．
【解析】试题分析：
（1）由题意设抛物线方程为
，则准线方程为
，解得
，即可求解抛物线的方程；
（2）由
消去
得
，根据
，解得
且
，得到
，即可求解的值．
试题解析：
（1）由题意设抛物线方程为（
），其准线方程为
，
∵
到焦点的距离等于到其准线的距离，∴
，∴，
∴此抛物线的方程为．
（2）由
消去得
，
∵直线
与抛物线相交于不同两点、，则有
解得
且，
由
，解得
或
（舍去）．
∴所求的值为2．
【题型】解答题
【结束】
20
【题目】如图，在四棱锥
中，底面
是平行四边形， 
，侧面
底面
， 
， 
， 
， 
分别为
， 
的中点，点
在线段
上．
（1）求证： 
平面
；
（2）如果三棱锥
的体积为
，求点
到面
的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）=aln（x2+1）+bx存在两个极值点x1 ， x2 ．
（1）求证：|x1+x2|＞2；
（2）若实数λ满足等式f（x1）+f（x2）+a+λb=0，试求λ的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
