
【题目】如图,已知过点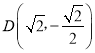 的椭圆
的椭圆![]() 的离心率为
的离心率为![]() ,左顶点和上顶点分别为A,B.
,左顶点和上顶点分别为A,B.
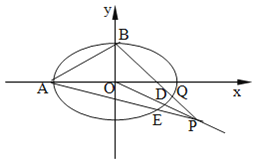
(1)求椭圆的标准方程;
(2)若P为线段OD延长线上一点,直线PA交椭圆于另一点E,直线PB交椭圆于另一点Q.
①求直线PA与PB的斜率之积;
②判断直线AB与EQ是否平行?并说明理由.
【答案】(1)![]() 1.(2) ①
1.(2) ① ![]() .②平行.理由见解析
.②平行.理由见解析
【解析】
(1)离心率值转化为![]() 关系,再把点
关系,再把点![]() 坐标代入方程,即可求出椭圆标准方程;
坐标代入方程,即可求出椭圆标准方程;
(2)①求出![]() 方程,设出
方程,设出![]() 点坐标,可求出直线PA与PB的斜率之积;
点坐标,可求出直线PA与PB的斜率之积;
②求出直线![]() 方程,分别与椭圆方程联立,求出
方程,分别与椭圆方程联立,求出![]() 两点坐标,代入斜率公式,求出直线
两点坐标,代入斜率公式,求出直线![]() 的斜率,然后再判断与直线
的斜率,然后再判断与直线![]() 是否平行.
是否平行.
(1)∵椭圆过点D(![]() ,
,![]() ),且离心率为
),且离心率为![]()
![]()
∴![]() ,
,
∴椭圆的方程为![]() 1.
1.
(2)①由(1)知A(﹣2,0),B(0,1),
直线OD方程为y![]() ,
,
点P在直线OD上,设P(﹣2y0,y0),
kPAkPB![]() .
.
②设E(x1,y1),Q(x2,y2),
联立直线AP:y![]() 与椭圆的方程得,
与椭圆的方程得,
(2y02﹣2y0+1)x2+4y02x+8y0﹣4=0,
∴﹣2+x1![]() ,
,
∴x1![]() ,y1
,y1![]() ,
,
联立直线BP:y![]() 与椭圆的方程得,
与椭圆的方程得,
![]() ,
,
∴x2![]() ,y2
,y2![]() ,
,
∴![]()
又因为kAB![]() ,∴kAB=kEQ,
,∴kAB=kEQ,
∴直线AB与EQ是平行.


科目:高中数学 来源: 题型:
【题目】某兴趣小组在科学馆的帕斯卡三角仪器前进行探究实验.如图所示,每次使一个实心小球从帕斯卡三角仪器的顶部入口落下,当它在依次碰到每层的菱形挡板时,会等可能地向左或者向右落下,在最底层的7个出口处各放置一个容器接住小球,该小组连续进行200次试验,并统计容器中的小球个数得到柱状图:
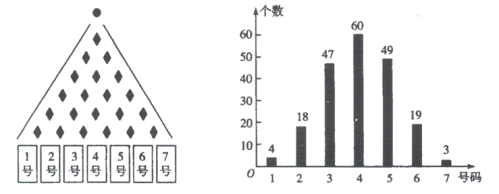
(Ⅰ)用该实验来估测小球落入4号容器的概率,若估测结果的误差小于![]() ,则称该实验是成功的.试问:该兴趣小组进行的实验是否成功?(误差
,则称该实验是成功的.试问:该兴趣小组进行的实验是否成功?(误差![]() )
)
(Ⅱ)再取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.(计算时采用概率的理论值)
的分布列与数学期望.(计算时采用概率的理论值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了节约用水,市民用水拟实行阶梯水价.每人月用水量中不超过![]() 立方米的部分按4元/立方米收费,超出
立方米的部分按4元/立方米收费,超出![]() 立方米的部分按10元/立方米收费.从该市随机调查了10 000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
立方米的部分按10元/立方米收费.从该市随机调查了10 000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:

(1)如果![]() 为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,
为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,![]() 至少定为多少?
至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替.当![]() =3时,试完成该10000位居民该月水费的频率分布表,并估计该市居民该月的人均水费.
=3时,试完成该10000位居民该月水费的频率分布表,并估计该市居民该月的人均水费.
组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
分组 |
|
|
|
|
|
|
|
|
频率 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右顶点为A,抛物线的焦点与点A重合.
的右顶点为A,抛物线的焦点与点A重合.
(1)求抛物线的标准方程;
(2)若直线l过点A且斜率为双曲线的离心率,求直线l被抛物线截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某老师是省级课题组的成员,主要研究课堂教学目标达成度,为方便研究,从实验班中随机抽取30次的随堂测试成绩进行数据分析![]() 已知学生甲的30次随堂测试成绩如下
已知学生甲的30次随堂测试成绩如下![]() 满分为100分
满分为100分![]() :
:

![]() 把学生甲的成绩按
把学生甲的成绩按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,列出频率分布表,并画出频率分布直方图;
分成6组,列出频率分布表,并画出频率分布直方图;
![]() 规定随堂测试成绩80分以上
规定随堂测试成绩80分以上![]() 含80分
含80分![]() 为优秀,为帮助学生甲提高成绩,选取学生乙,对甲与乙的随堂测试成绩进行对比分析,甲与乙测试成绩是否为优秀相互独立
为优秀,为帮助学生甲提高成绩,选取学生乙,对甲与乙的随堂测试成绩进行对比分析,甲与乙测试成绩是否为优秀相互独立![]() 已知甲成绩优秀的概率为
已知甲成绩优秀的概率为![]() 以频率估计概率
以频率估计概率![]() ,乙成绩优秀的概率为
,乙成绩优秀的概率为![]() ,若
,若![]() ,则此二人适合为学习上互帮互助的“对子”
,则此二人适合为学习上互帮互助的“对子”![]() 在一次随堂测试中,记
在一次随堂测试中,记![]() 为两人中获得优秀的人数,已知
为两人中获得优秀的人数,已知![]() ,问二人是否适合结为“对子”?
,问二人是否适合结为“对子”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工企业2018年年底投入100万元,购入一套污水处理设备。该设备每年的运转费用是0.5万元,此外,每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元。设该企业使用该设备![]() 年的年平均污水处理费用为
年的年平均污水处理费用为![]() (单位:万元)
(单位:万元)
(1)用![]() 表示
表示![]() ;
;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备。则该企业几年后需要重新更换新的污水处理设备。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,过坐标原点
,过坐标原点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() .连结
.连结![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com